You are here
Ex 6.3, 2 - Chapter 6 Class 10 Triangles
Last updated at July 20, 2026 by Teachoo
Given similar, find angles or sides
Chapter 6 Class 10 Triangles
Concept wise
Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 5 questions, selected from your answers, mistakes, and progress.
🎉 Smart choice! You just saved 2+ minutes of ads and got straight to the good stuff. That's what being a Teachoo Black member is all about.
Transcript
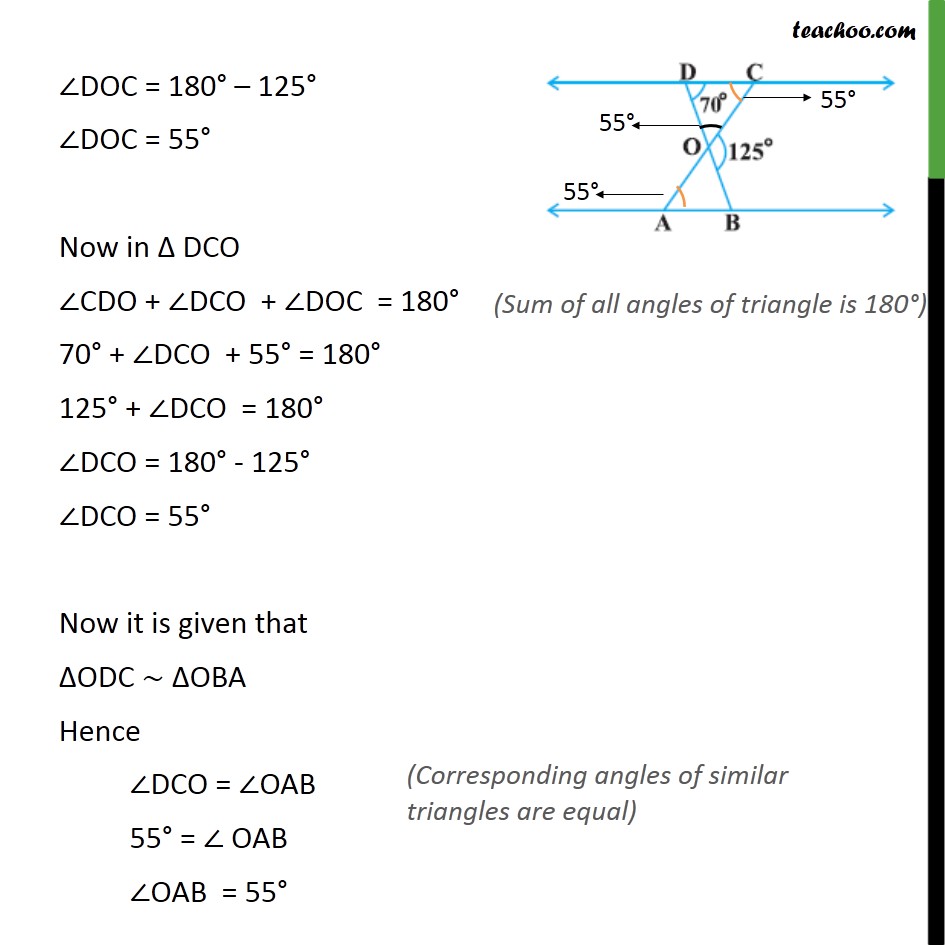
Ex 6.3, 2 In figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB. Given: Δ ODC ∼ Δ OBA ∠ BOC = 125° ∠ CDO = 70° To find: ∠DOC, ∠DCO and ∠OAB Solution: Here, BD is a line, So, we can apply linear pair on it. ∠BOC + ∠DOC = 180° 125° + ∠DOC = 180° ∠DOC = 180° – 125° ∠DOC = 180° – 125° ∠DOC = 55° Now in Δ DCO ∠CDO + ∠DCO + ∠DOC = 180° 70° + ∠DCO + 55° = 180° 125° + ∠DCO = 180° ∠DCO = 180° - 125° ∠DCO = 55° Now it is given that ΔODC ∼ ΔOBA Hence ∠DCO = ∠OAB 55° = ∠ OAB ∠OAB = 55°
