Example 8 - Chapter 4 Class 10 Quadratic Equations (Important Question)

Transcript

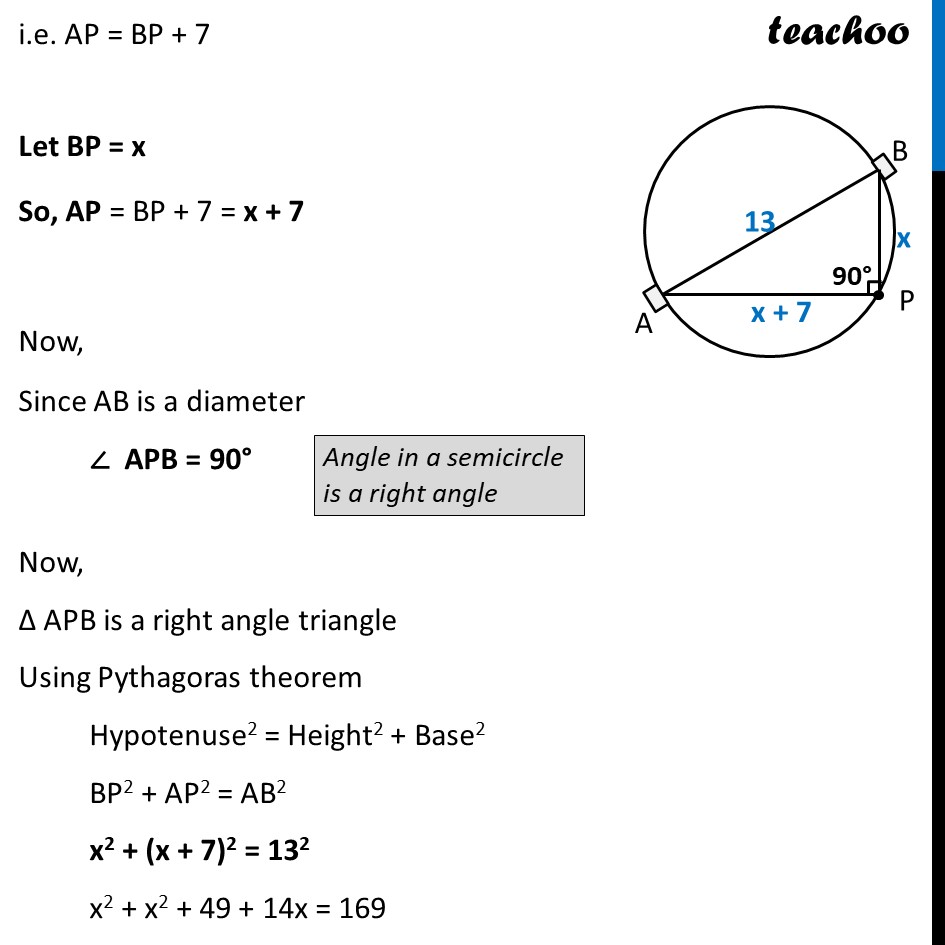
Example 8 A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected? Let P be the pole Gates A & B are diametrically opposite So, AB = Diameter of circle = 13 m Also given that, Difference of the distance of the pole from the two gates is 7 metres BP – AP or AP – BP is 7 m Let us take AP – BP = 7 i.e. AP = BP + 7 Let BP = x So, AP = BP + 7 = x + 7 Now, Since AB is a diameter ∠ APB = 90° Now, Δ APB is a right angle triangle Using Pythagoras theorem Hypotenuse2 = Height2 + Base2 BP2 + AP2 = AB2 x2 + (x + 7)2 = 132 x2 + x2 + 49 + 14x = 169 2x2 + 14x + 49 – 169 = 0 2x2 + 14x – 120 = 0 Divide the equation by 2 2𝑥2/2+14𝑥/2−120/2 = 0 x2 + 7x – 60 = 0 Comparing equation with ax2 + bx + c = 0 Here, a = 1, b = 7, c = – 60 We know that D = b2 – 4ac D = (7)2 – 4×(1)×(−60) = 49 – 4×(−60) = 49 + 240 = 289 Hence , roots to equation are x = (−𝑏 ± √𝐷)/2𝑎 Putting values x = (− 7 ± √289)/(2 × 1) x = (− 𝟕 ± 𝟏𝟕 )/𝟐 Solving So, x = 5, & x = –12 x = (−7 + 17)/2 x = 10/2 x = 5 x = (−7 −17)/2 x = (−24)/2 x = –12 Since x is distance, it must be positive Hence, x = 5. Hence, BP = x = 5 m & AP = x + 7 = 5 + 7 = 12 m