Question 4 - Past Year MCQ - Chapter 7 Class 10 Coordinate Geometry

Transcript

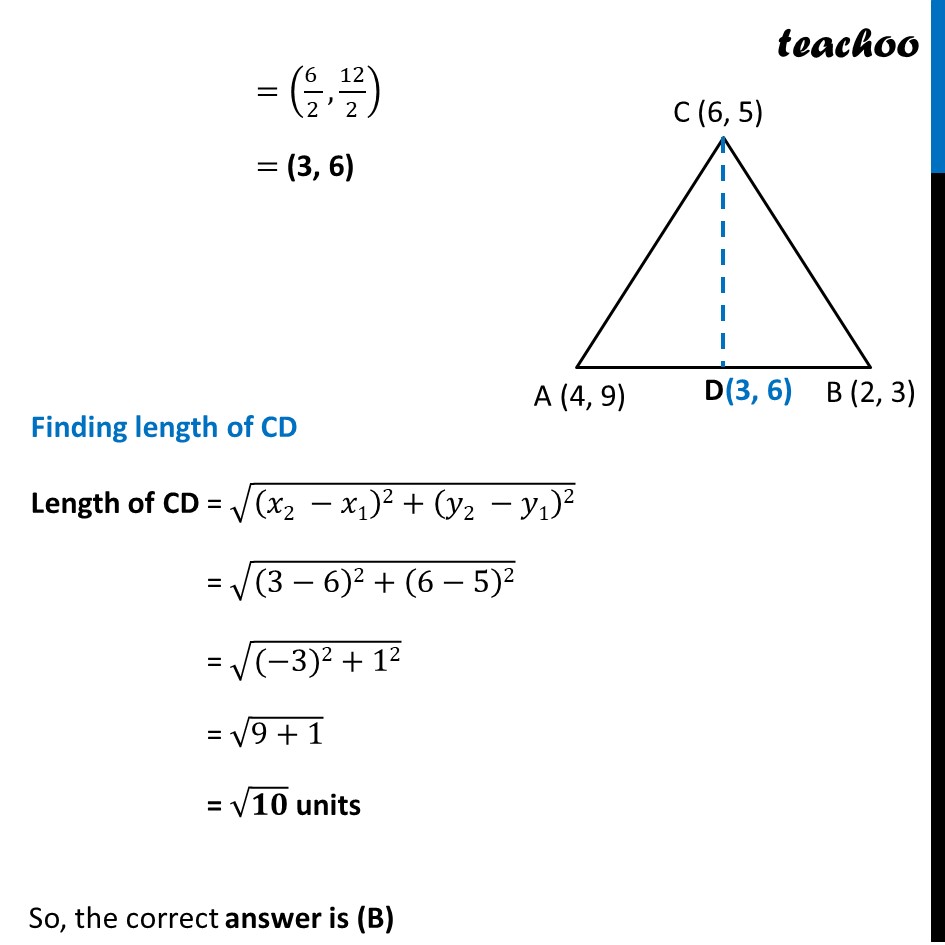
Question 4 If A (4, 9), B (2, 3) and C (6, 5) are the vertices of ∆ ABC, then the length of median through C is (A) 5 units (B) √10 units (C) 25 units (D) 10 Joining vertex C to line AB such that CD is the median Coordinates of D = Coordinates of Mid point of AB = ((4 + 2)/2,(9 + 3)/2) =((6 )/2,12/2) = (3, 6) Finding length of CD Length of CD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √((3−6)2+(6−5)2) = √((−3)2+12) = √(9+1) = √𝟏𝟎 units So, the correct answer is (B)