Question 2 - Graph of pair of Linear Equations - Chapter 3 Class 10 Pair of Linear Equations in Two Variables

Transcript

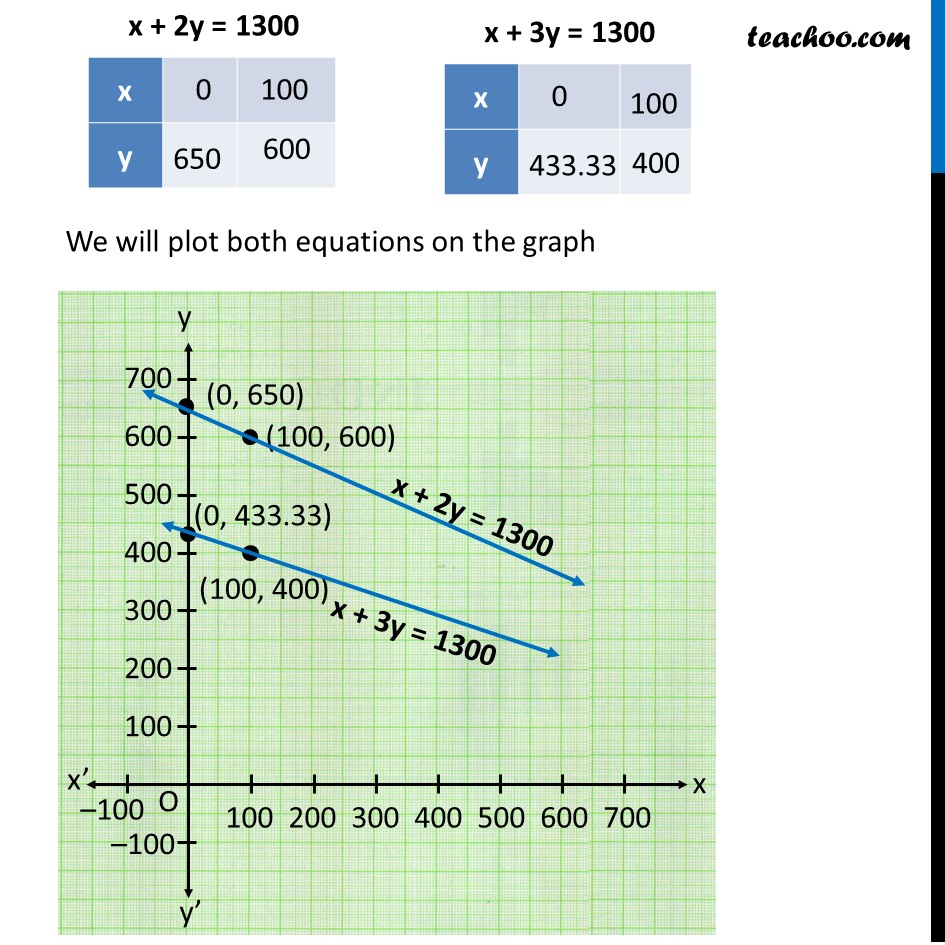
Question 2 The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically. Let the Cost of one bat be Rs x & let Cost of one ball be Rs y Given that 3 bats and 6 balls cost Rs 3900 3 × Cost of one bat + 6 × Cost of one ball = 3900 3x + 6y = 3900 3(x + 2y) = 3 × 1300 x + 2y = 1300 Also, She buys another bat and 3 more balls of the same kind for Rs 1300 1 × Cost of one bat + 3 × Cost of one ball = 1300 x + 3y = 1300 Now, plotting equations x + 2y = 1300 ...(1) x + 3y = 1300 ...(2) For Equation (1) x + 2y = 1300 Let x = 0 0 + 2y = 1300 2y = 1300 y = 1300/2 y = 650 So, x = 0, y = 650 is a solution i.e. (0, 650) is a solution Let x = 100 100 + 2y = 1300 2y = 1300 − 100 y = 1200/2 y = 600 So, x = 100, y = 600 is a solution i.e. (100, 600) is a solution For Equation (2) x + 3y = 1300 Let x = 0 0 + 3y = 1300 3y = 1300 y = 1300/3 y = 433.3 So, x = 0, y = 433.33.. is a solution i.e. (0, 433.33..) is a solution Let x = 100 100 + 3y = 1300 3y = 1300 − 100 y = 1200/3 y = 400 So, x = 100, y = 400 is a solution i.e. (100, 400) is a solution We will plot both equations on the graph