1. Class 10
  2. Solutions of Sample Papers for Class 10 Boards
  3. CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [MCQ]

Question 34 - CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [MCQ] - Solutions of Sample Papers for Class 10 Boards

Last updated at Sept. 6, 2021 by

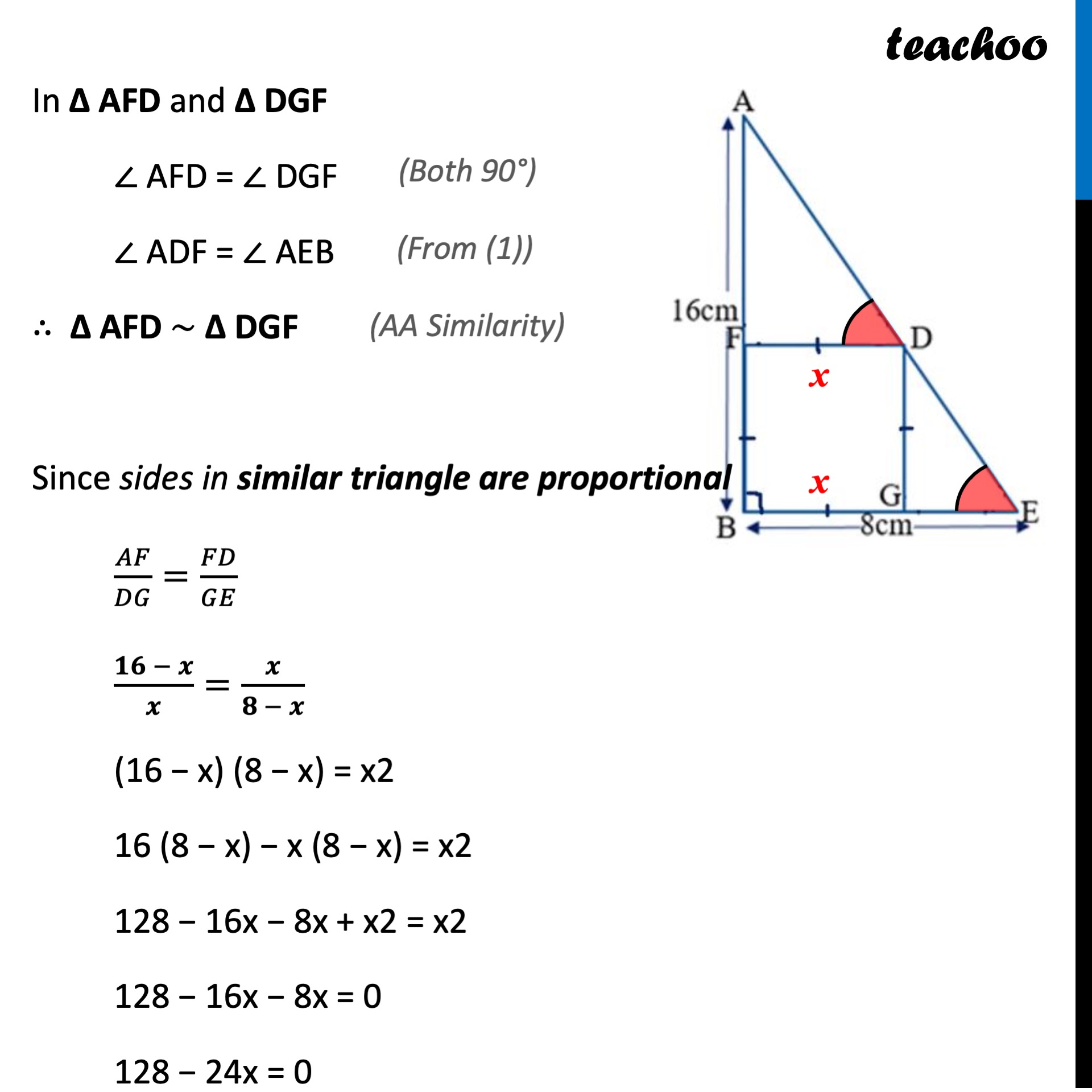
Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is

(a) 13/100  (b) 13/10    (c) 10/13   (d) 100/13

Slide72.jpeg

Advertisement

Slide73.jpeg

Advertisement

Slide74.jpeg

  1. Class 10
  2. Solutions of Sample Papers for Class 10 Boards

    3. CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [MCQ]

    CBSE Class 10 Sample Paper for 2022 Boards - Maths Basic [MCQ] →

Transcript

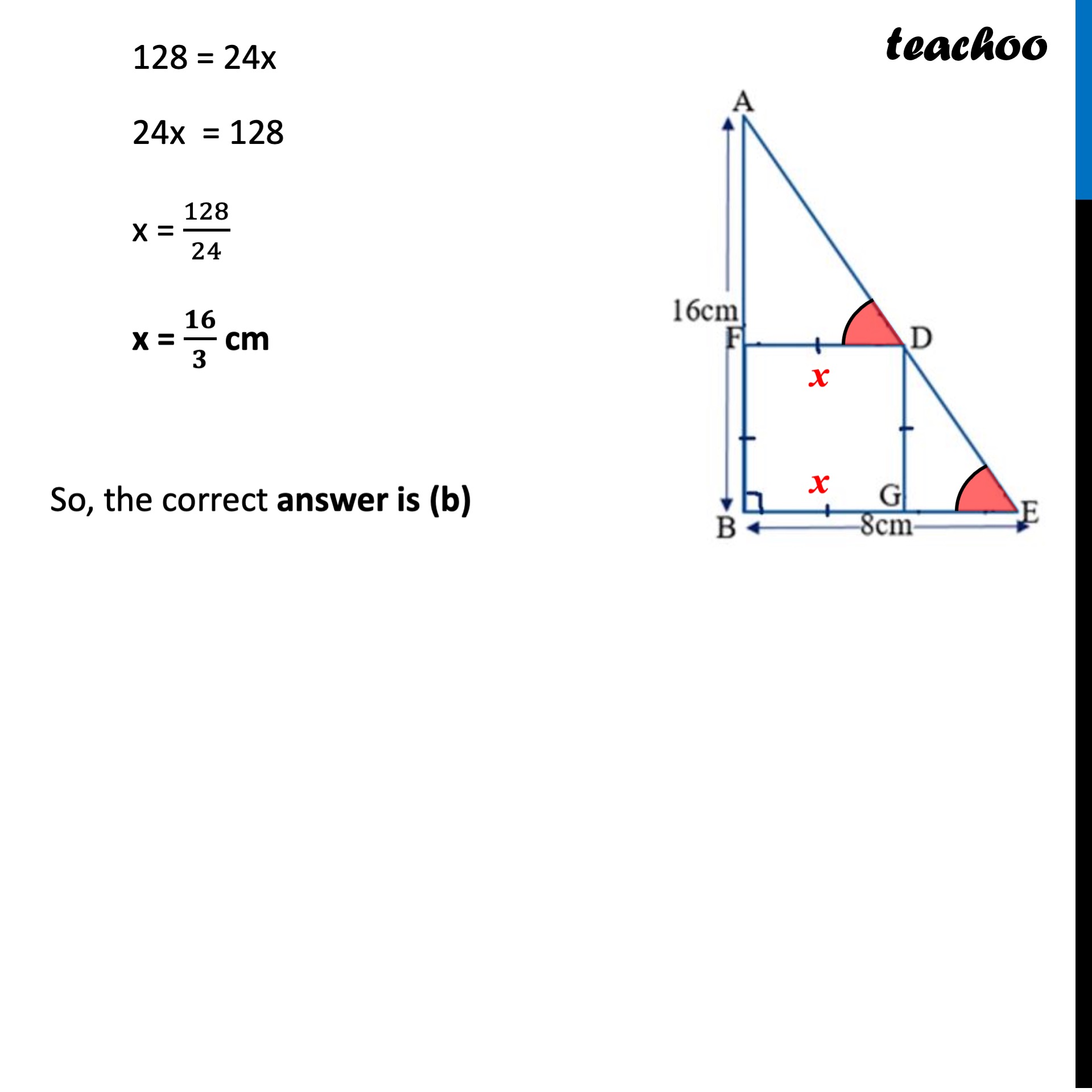
Question 34 Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is (a) 13/100 (b) 13/10 (c) 10/13 (d) 100/13 Let FDGB be a square with side x cm Now, For parallel lines FD and CE with transversal AE ∠ ADF = ∠ AEB Also, since FDGB is a square ∠ AFD = 90° & ∠ DGF = 90° In Δ AFD and Δ DGF ∠ AFD = ∠ DGF ∠ ADF = ∠ AEB ∴ Δ AFD ~ Δ DGF Since sides in similar triangle are proportional 𝐴𝐹/𝐷𝐺=𝐹𝐷/𝐺𝐸 (𝟏𝟔 − 𝒙)/𝒙=𝒙/(𝟖 − 𝒙) (16 − x) (8 − x) = x2 16 (8 − x) − x (8 − x) = x2 128 − 16x − 8x + x2 = x2 128 − 16x − 8x = 0 128 − 24x = 0 128 = 24x 24x = 128 x = 128/24 x = 𝟏𝟔/𝟑 cm So, the correct answer is (b)

Class 10
Solutions of Sample Papers for Class 10 Boards

About the Author

Davneet Singh's photo - Teacher, Engineer, Marketer
Davneet Singh
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur. He has been teaching from the past 10 years. He provides courses for Maths and Science at Teachoo.