Ex 1.2, 2 - Chapter 1 Class 10 Real Numbers

Transcript

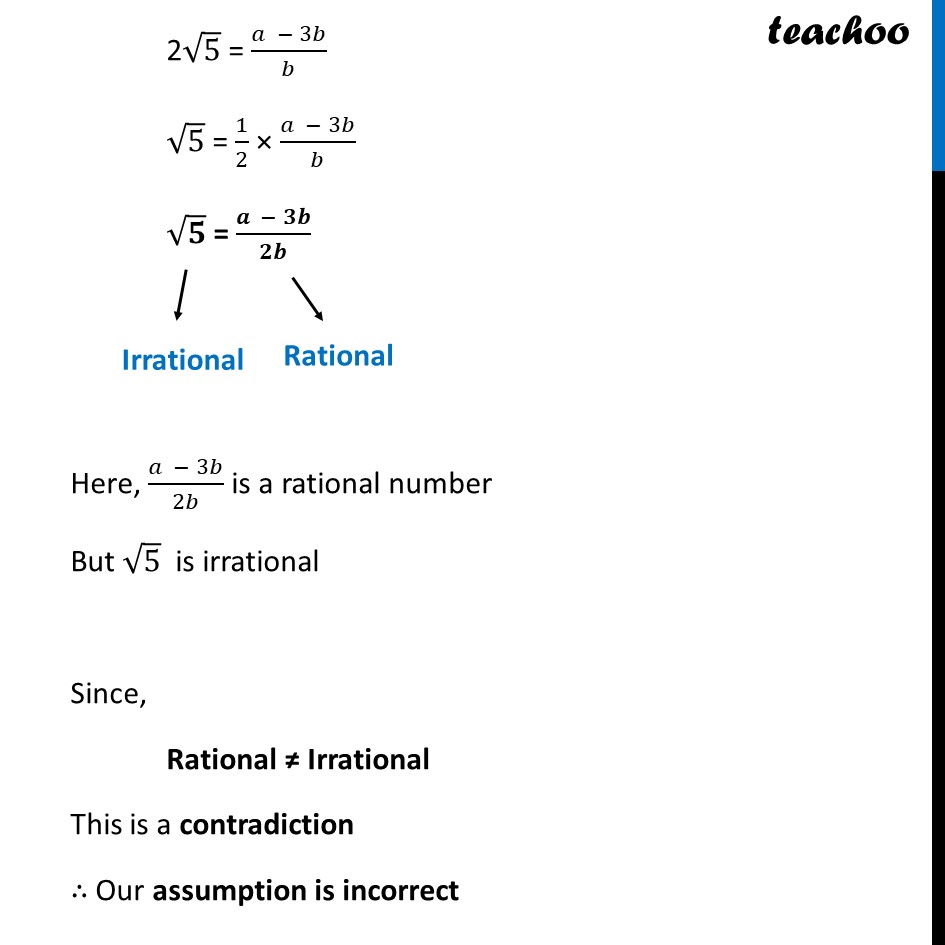
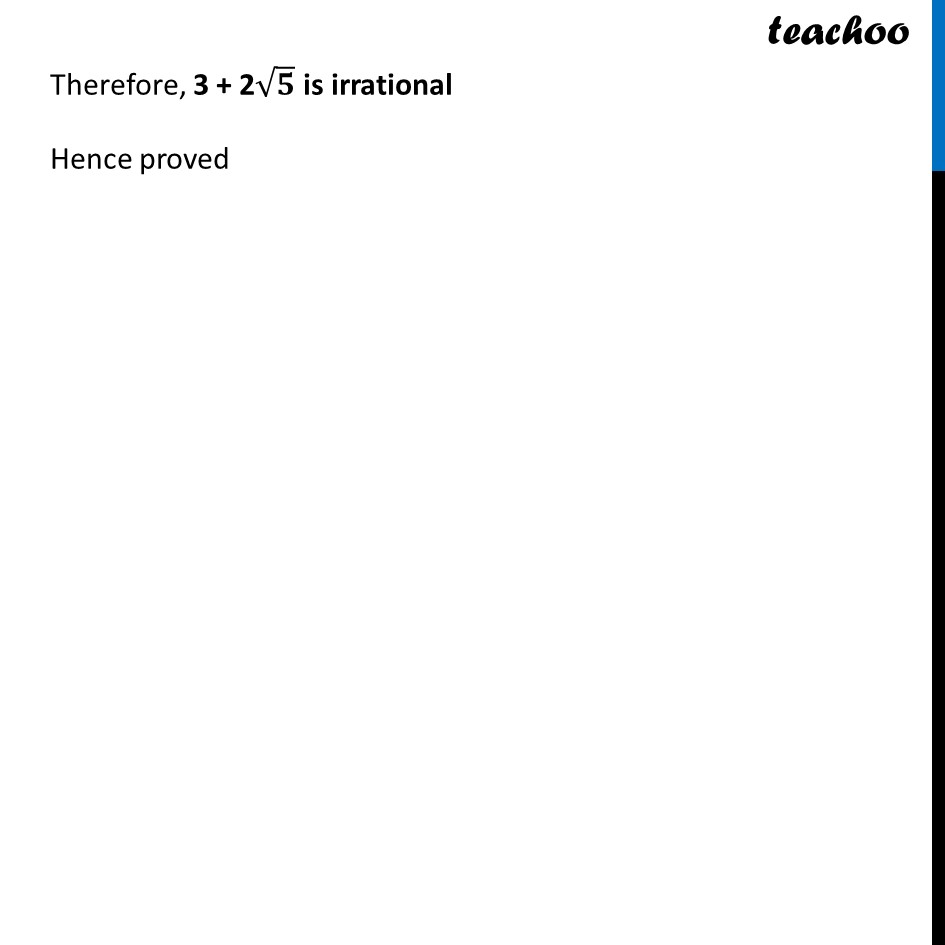
Ex 1.2, 2 Prove that 3 + 2√5 is irrational. We have to prove 3 + 2√5 is irrational Let us assume the opposite, i.e., 3 + 2√𝟓 is rational Hence, 3 + 2√5 can be written in the form 𝑎/𝑏 where a and b (b≠ 0) are co-prime (no common factor other than 1) Hence, 3 + 2√𝟓 = 𝒂/𝒃 2√5 = 𝑎/𝑏 − 3 2√5 = (𝑎 − 3𝑏)/𝑏 2√5 = (𝑎 − 3𝑏)/𝑏 √5 = 1/2 × (𝑎 − 3𝑏)/𝑏 √𝟓 = (𝒂 − 𝟑𝒃)/𝟐𝒃 Here, (𝑎 − 3𝑏)/2𝑏 is a rational number But √5 is irrational Since, Rational ≠ Irrational This is a contradiction ∴ Our assumption is incorrect Therefore, 3 + 2√𝟓 is irrational Hence proved