Example 6 (Shortcut Method) - Chapter 13 Class 11 Statistics
Last updated at Dec. 16, 2024 by Teachoo
Examples
Example 1
You are here
You are here
Chapter 13 Class 11 Statistics
Serial order wise
Transcript
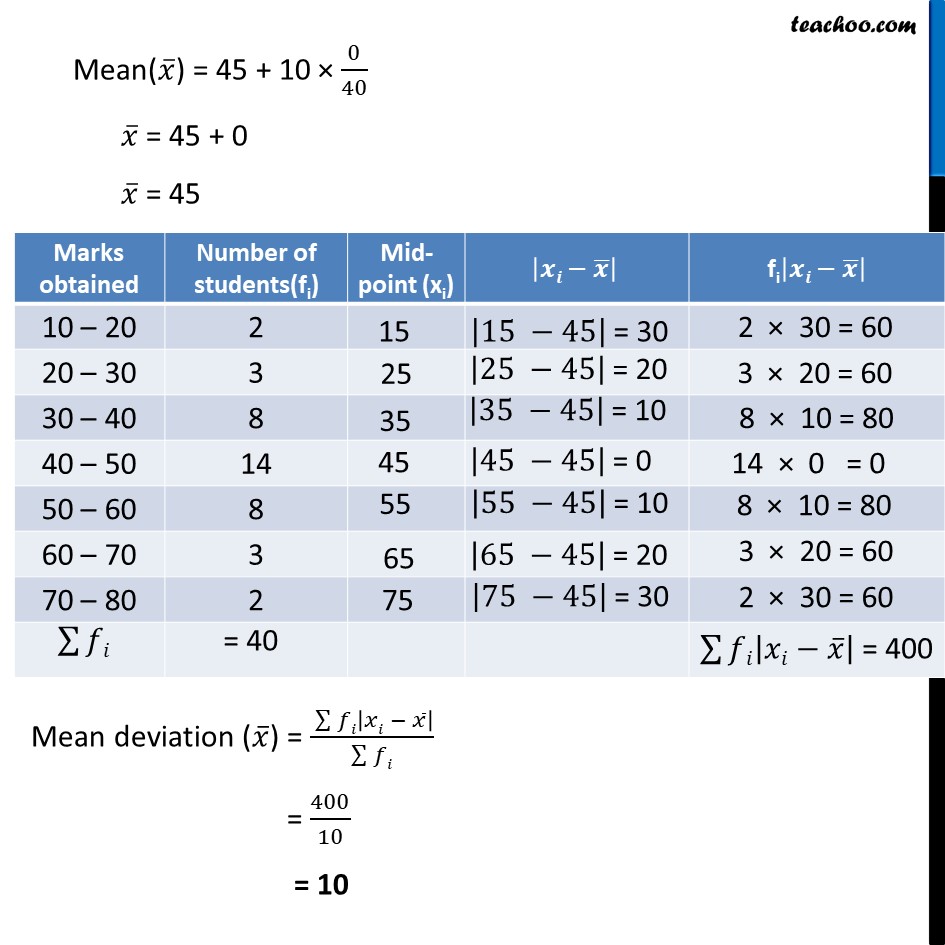
Example 6 (shortcut method) Find the mean deviation about the mean for the following data. Mean(𝑥 ̅) = a + h × (∑▒𝑓𝑖𝑑𝑖)/(∑▒𝑓𝑖) Here, a = assumed mean = 45 h = width of class = 10 𝑑_𝑖= (𝑥_𝑖− 𝑎)/ℎ Marks obtained Number of students(fi) Mid-point (xi) xi – a = (xi – 45) di = "xi – a" /h fidi 10 – 20 2 20 – 30 3 30 – 40 8 40 – 50 14 50 – 60 8 60 – 70 3 70 – 80 2 40 Marks obtained Number of students(fi) Mid-point (xi) xi – a = (xi – 45) di = "xi – a" /h fidi 10 – 20 2 20 – 30 3 30 – 40 8 40 – 50 14 50 – 60 8 60 – 70 3 70 – 80 2 40 Mean(𝑥 ̅) = 45 + 10 × 0/40 𝑥 ̅ = 45 + 0 𝑥 ̅ = 45 Marks obtained Number of students(fi) Mid-point (xi) |xi-x ̅ | fi|xi-x ̅ | 10 – 20 2 20 – 30 3 30 – 40 8 40 – 50 14 50 – 60 8 60 – 70 3 70 – 80 2 Mean deviation (𝑥 ̅) = ( ∑128▒𝑓𝑖|𝑥𝑖 − 𝑥 ̅ | )/(∑128▒𝑓𝑖) = 400/10 = 10
