Ex 12.2, 11 (ii) - Chapter 12 Class 11 Limits and Derivatives

Last updated at April 16, 2024 by

Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 3

Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 4
Ex 13.2, 11 - Chapter 13 Class 11 Limits and Derivatives - Part 5

Transcript

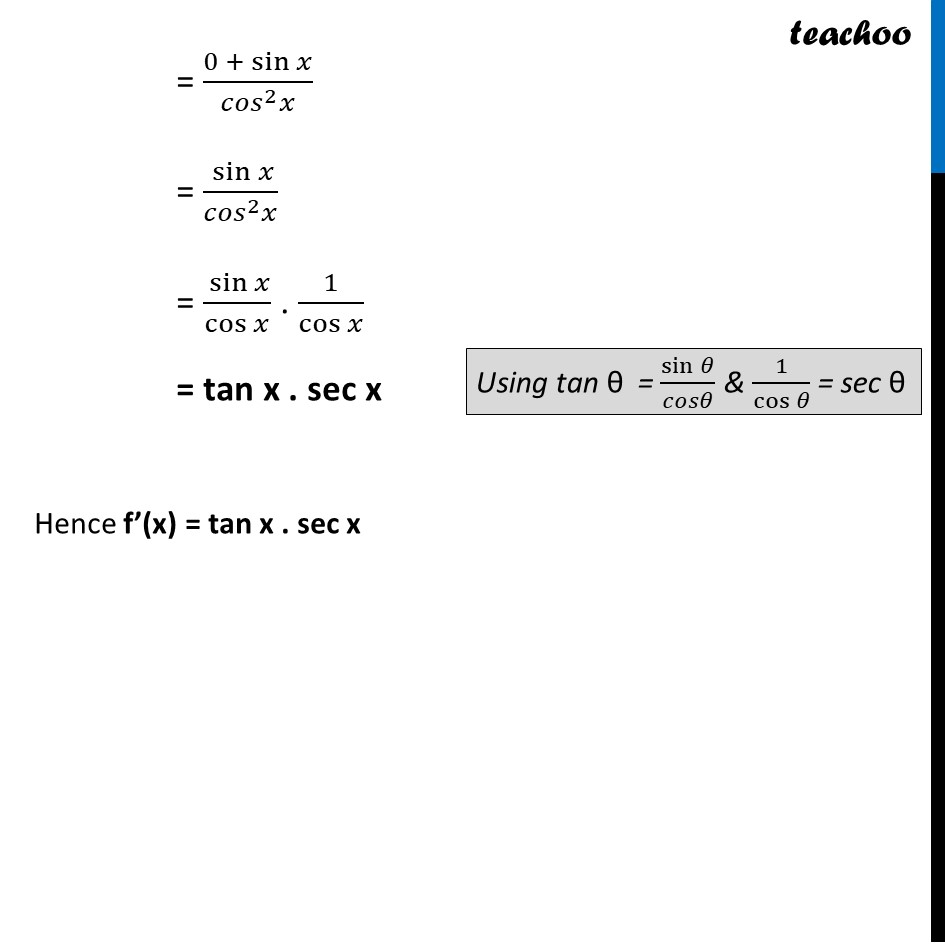
Ex 12.2, 11 Find the derivative of the following functions: (ii) sec x Let f (x) = sec x f(x) = 1/cos⁡𝑥 Let u = 1 & v = cos x So, f(x) = 𝑢/𝑣 ∴ f’(x) = (𝑢/𝑣)^′ Using quotient rule f’(x) = (𝑢^′ 𝑣 − 𝑣^′ 𝑢)/𝑣^2 Finding u’ & v’ u = 1 u’ = 0 & v = cos x v’ = – sin x Now, f’(x) = (𝑢^′ 𝑣 − 𝑣^′ 𝑢)/𝑣^2 = (0(cos⁡〖𝑥) − (−sin⁡〖𝑥) (1)〗 〗)/(〖𝑐𝑜𝑠〗^2 𝑥) (Derivative of constant is 0) (Derivative of cos x = – sin x) = (0 +〖 sin〗⁡𝑥)/(〖𝑐𝑜𝑠〗^2 𝑥) = 〖 sin〗⁡𝑥/(〖𝑐𝑜𝑠〗^2 𝑥) = 〖 sin〗⁡𝑥/cos⁡𝑥 . 1/cos⁡𝑥 = tan x . sec x Hence f’(x) = tan x . sec x Using tan θ = sin⁡𝜃/𝑐𝑜𝑠𝜃 & 1/cos⁡𝜃 = sec θ

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.