Last updated at Dec. 16, 2024 by Teachoo
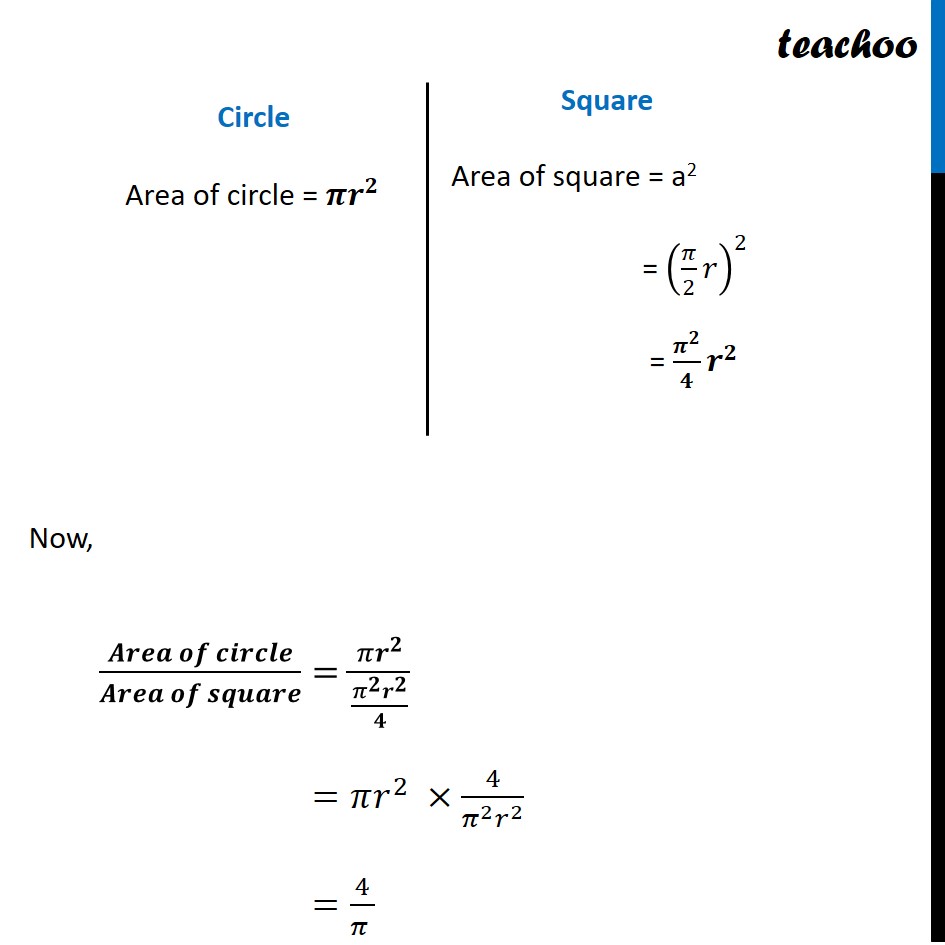
Question 7 If the perimeter of a circle is equal to that of a square, then the ratio of their areas is (A) 22 : 7 (B) 14 : 11 (C) 7 : 22 (D) 11: 14 Let Radius of circle = r Side of square = a Now, given that Circumference of Circle = Perimeter of Square 2𝜋r = 4a 𝜋r = 2a 2a = 𝜋r a = 𝝅/𝟐 𝒓 Now, we need to find ratio between Area of square and circle Circle Area of circle = 𝝅𝒓^𝟐 Square Area of square = a2 = (𝜋/2 𝑟)^2 = 𝝅^𝟐/𝟒 𝒓^𝟐 Now, (𝑨𝒓𝒆𝒂 𝒐𝒇 𝒄𝒊𝒓𝒄𝒍𝒆)/(𝑨𝒓𝒆𝒂 𝒐𝒇 𝒔𝒒𝒖𝒂𝒓𝒆)=(𝜋𝒓^𝟐)/((𝜋^𝟐 𝒓^𝟐)/𝟒) =𝜋𝑟^2 ×4/(𝜋^2 𝑟^2 ) =4/(𝜋 ) =4/(22/7) =(4 × 7)/22 =(2 × 7)/11 =𝟏𝟒/𝟏𝟏 ∴ Required ratio is 14 : 11 So, the correct answer is (B) =4/(22/7) =(4 × 7)/22 =(2 × 7)/11 =𝟏𝟒/𝟏𝟏 ∴ Required ratio is 14 : 11 So, the correct answer is (B) =4/(22/7) =(4 × 7)/22 =(2 × 7)/11 =𝟏𝟒/𝟏𝟏 ∴ Required ratio is 14 : 11 So, the correct answer is (B)
You are here