Question 15 - NCERT Exemplar - MCQ - Chapter 7 Class 10 Coordinate Geometry

Transcript

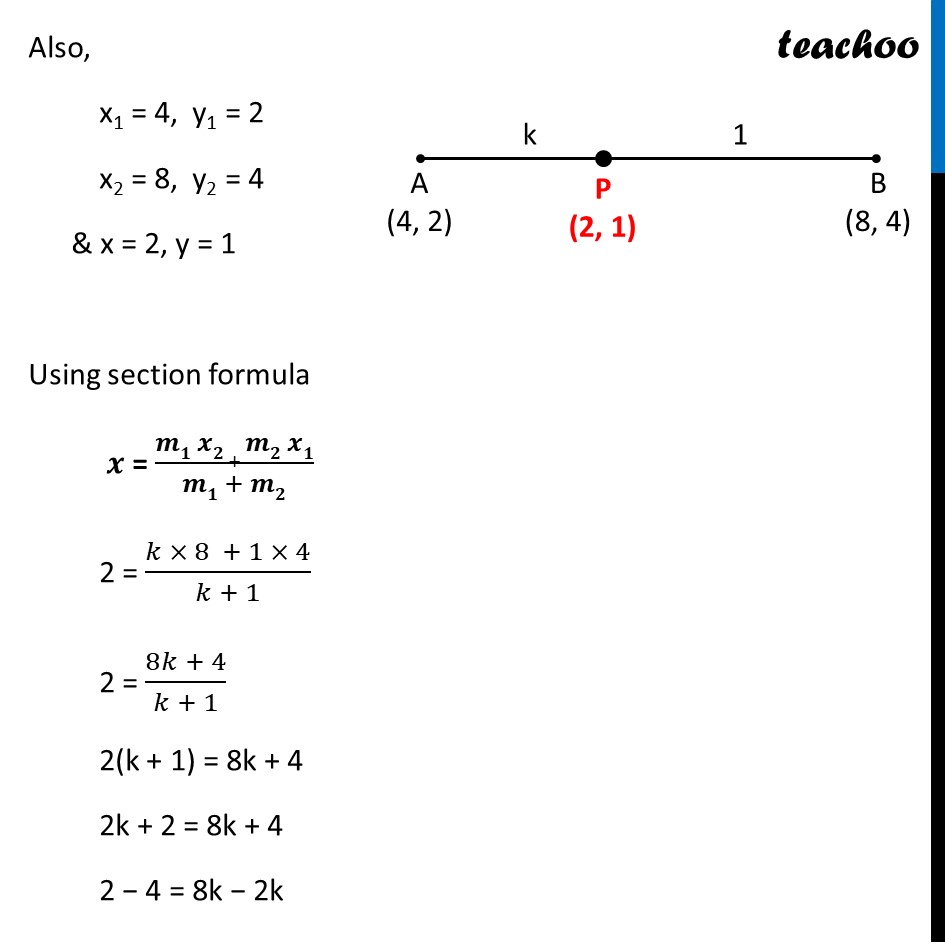
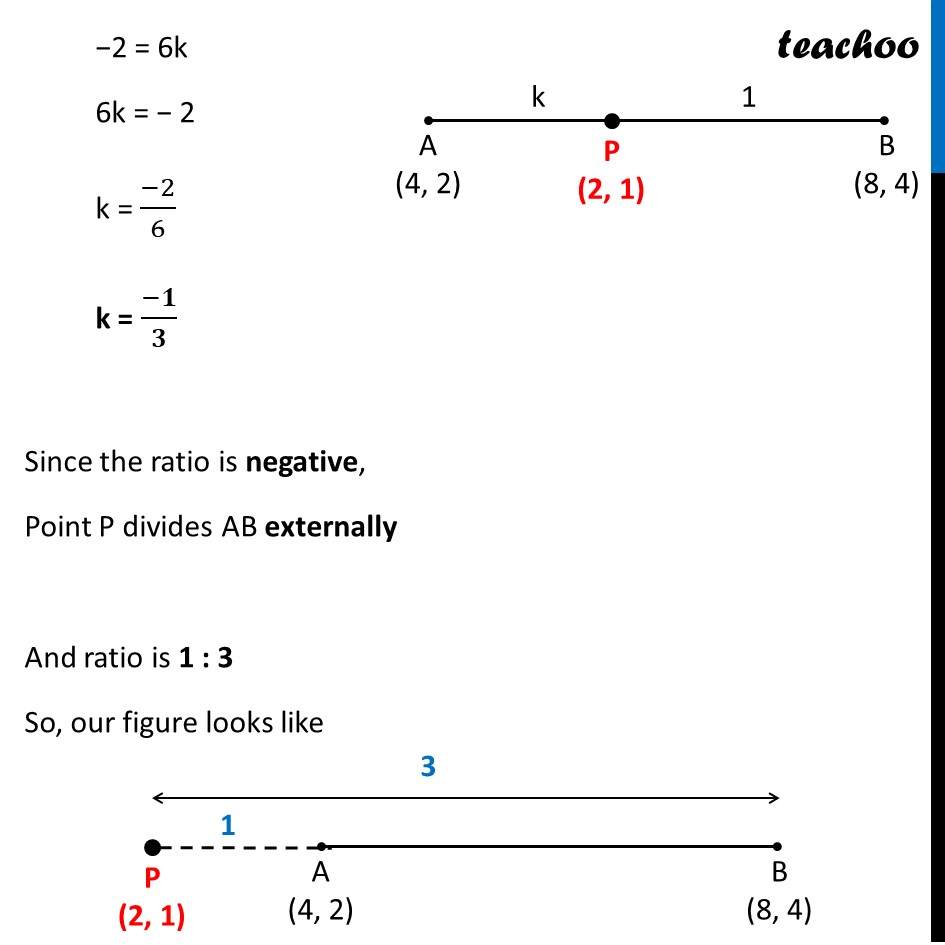
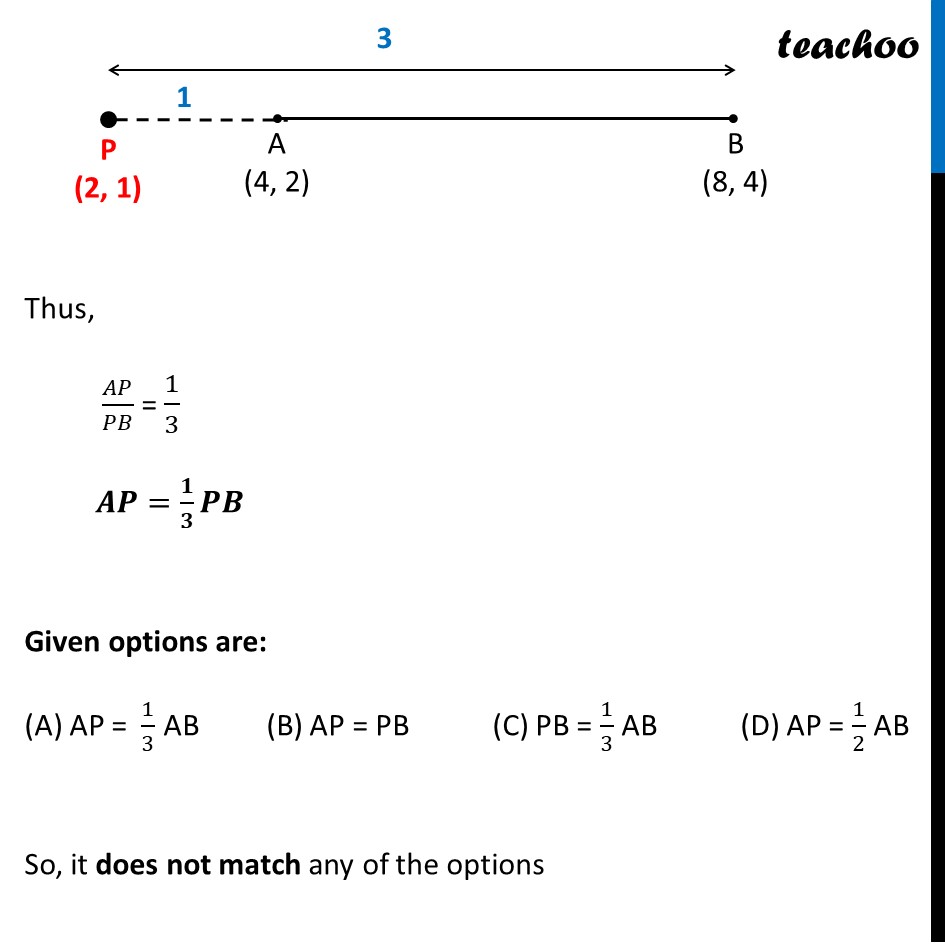
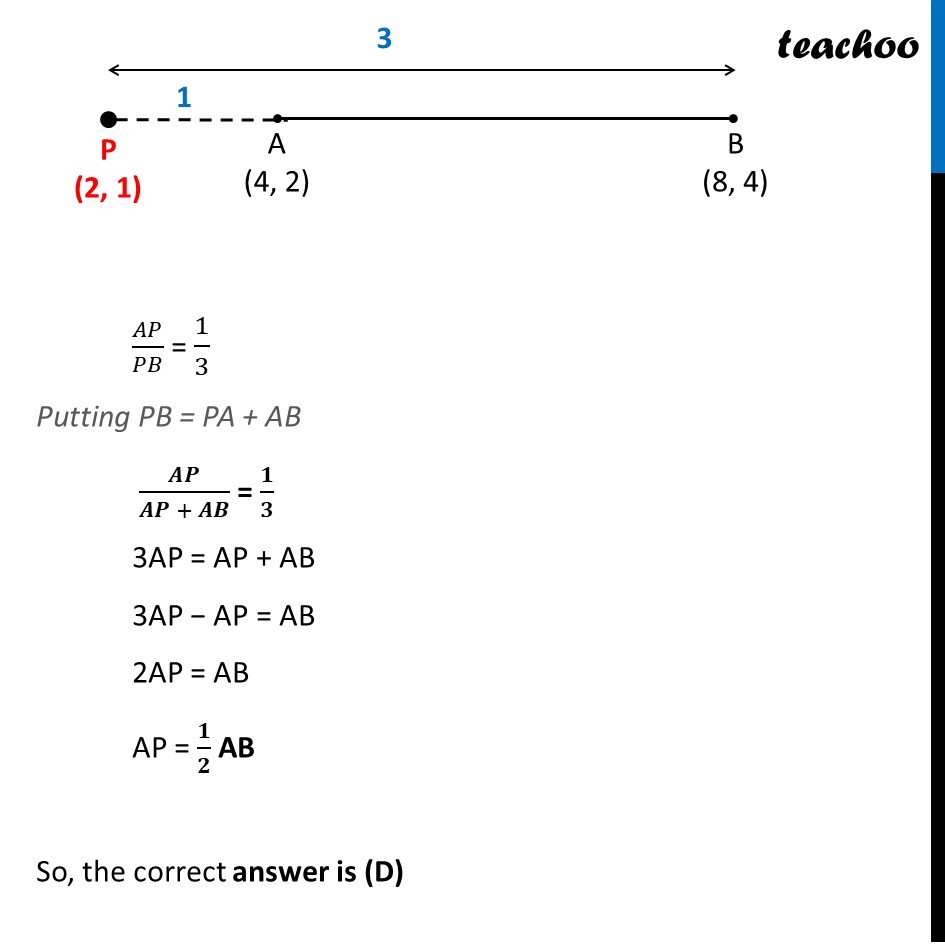
Question 15 If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4), then (A) AP = 1/3 AB (B) AP = PB (C) PB = 1/3 AB (D) AP = 1/2 AB We need to find ratio between AP & PB Let the ratio be k : 1 Also, x1 = 4, y1 = 2 x2 = 8, y2 = 4 & x = 2, y = 1 Using section formula 𝒙 = (𝒎𝟏 𝒙𝟐 + 𝒎𝟐 𝒙𝟏)/(𝒎𝟏 + 𝒎𝟐) 2 = (𝑘 × 8 + 1 × 4)/(𝑘 + 1) 2 = (8𝑘 + 4)/(𝑘 + 1) 2(k + 1) = 8k + 4 2k + 2 = 8k + 4 2 − 4 = 8k − 2k −2 = 6k 6k = − 2 k = (−2)/6 k = (−𝟏)/𝟑 Since the ratio is negative, Point P divides AB externally And ratio is 1 : 3 So, our figure looks like Thus, 𝐴𝑃/𝑃𝐵 = 1/3 𝑨𝑷=𝟏/𝟑 𝑷𝑩 Given options are: (A) AP = 1/3 AB (B) AP = PB (C) PB = 1/3 AB (D) AP = 1/2 AB So, it does not match any of the options 𝐴𝑃/𝑃𝐵 = 1/3 Putting PB = PA + AB 𝑨𝑷/(𝑨𝑷 + 𝑨𝑩) = 𝟏/𝟑 3AP = AP + AB 3AP − AP = AB 2AP = AB AP = 𝟏/𝟐 AB So, the correct answer is (D)