Check sibling questions

Question 4 - NCERT Exemplar - MCQ - Chapter 6 Class 10 Triangles (Term 1)

Last updated at Oct. 20, 2021 by

The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is

(A) 9 cm  

(B) 10 cm

(C) 8 cm 

(D) 20 cm

This question is inspired from  Ex 6.5, 7 - Chapter 6 Class 10 - Triangles

Slide8.JPG

Slide9.JPG
Slide10.JPG

This video is only available for Teachoo black users

Subscribe Now

Introducing your new favourite teacher - Teachoo Black, at only ₹83 per month

Join Teachoo Black

Transcript

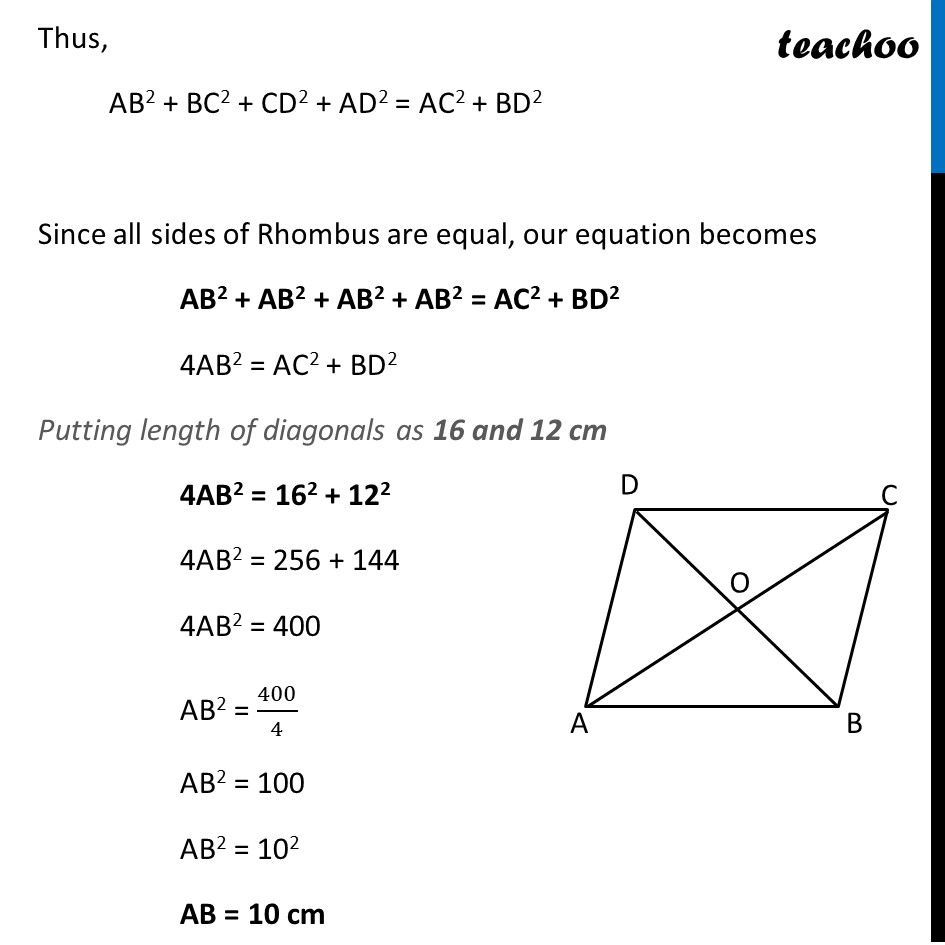
Question 4 The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is 9 cm (B) 10 cm (C) 8 cm (D) 20 cm In a Rhombus Sum of squares of sides = Sum of its diagonals (For proof, check Ex 6.5, 7 – Chapter 6 Class 10 Triangles) Thus, AB2 + BC2 + CD2 + AD2 = AC2 + BD2 Since all sides of Rhombus are equal, our equation becomes AB2 + AB2 + AB2 + AB2 = AC2 + BD2 4AB2 = AC2 + BD2 Putting length of diagonals as 16 and 12 cm 4AB2 = 162 + 122 4AB2 = 256 + 144 4AB2 = 400 AB2 = 400/4 AB2 = 100 AB2 = 102 AB = 10 cm So, the correct answer is (B) So, the correct answer is (B)

Davneet Singh's photo - Teacher, Engineer, Marketer

Made by

Davneet Singh

Davneet Singh is a graduate from Indian Institute of Technology, Kanpur. He has been teaching from the past 12 years. He provides courses for Maths and Science at Teachoo.