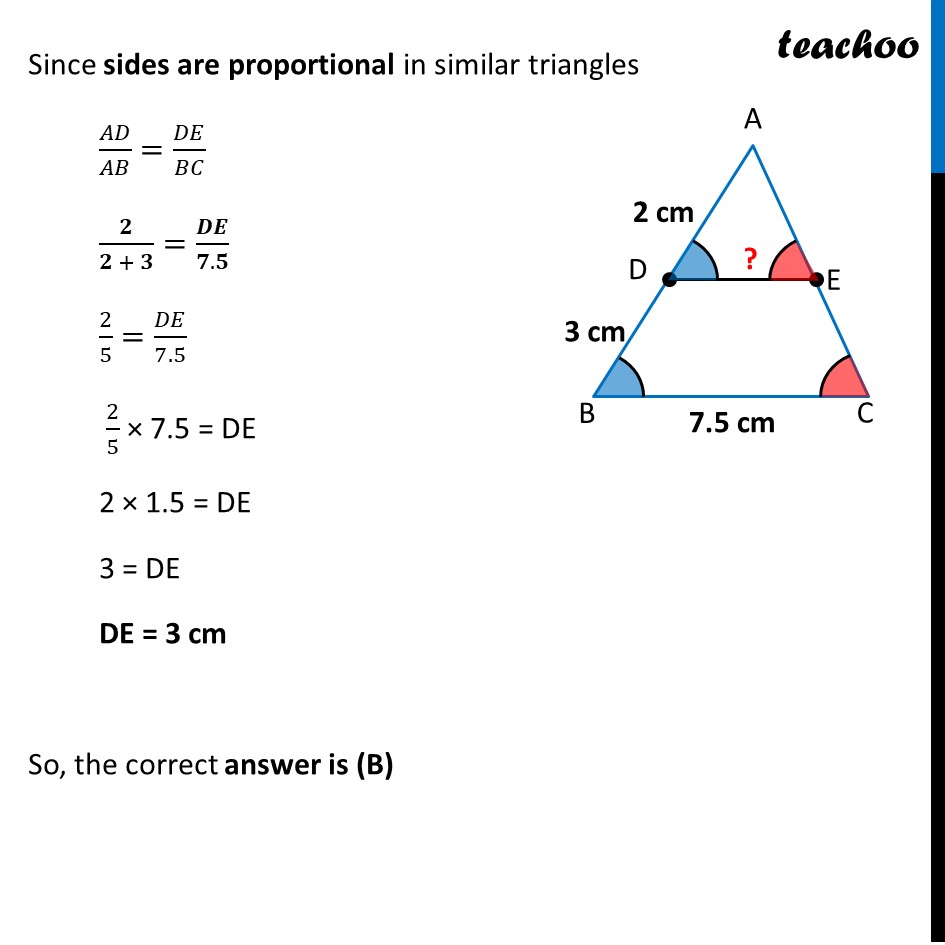
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE ∥ BC. Then, length of DE (in cm) is
(A) 2.5
(B) 3
(C) 5
(D) 6
Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 3 questions, selected from your answers, mistakes, and progress.
Question 2
D and E are respectively the points on the sides AB and AC of
a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE ∥ BC. Then, length of DE (in cm) is
(A) 2.5 (B) 3 (C) 5 (D) 6
Since DE ∥ BC
∠ ADB = ∠ ABD
∠ AED = ∠ ACB
Thus, by AA Similarity
Δ ADE ~ Δ ABC
(Corresponding angles)
(Corresponding angles)
Since sides are proportional in similar triangles
𝐴𝐷/𝐴𝐵=𝐷𝐸/𝐵𝐶
𝟐/(𝟐 + 𝟑)=𝑫𝑬/(𝟕.𝟓)
2/5=𝐷𝐸/7.5
2/5 × 7.5 = DE
2 × 1.5 = DE
3 = DE
DE = 3 cm
So, the correct answer is (B)
Made by
Davneet Singh
Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.
Many students prefer Teachoo Black for a smooth, ad-free learning experience.
It looks like you're using AdBlock
Don't be a miser! Join Teachoo Black at ₹19 only to view the ad-free version of Teachoo.
Please login to view more pages. It's free :)
Teachoo gives you a better experience when you're logged in. Please login :)
You are here
