Question 3 - Chapter 12 Class 9 Herons Formula (Important Question)

Transcript

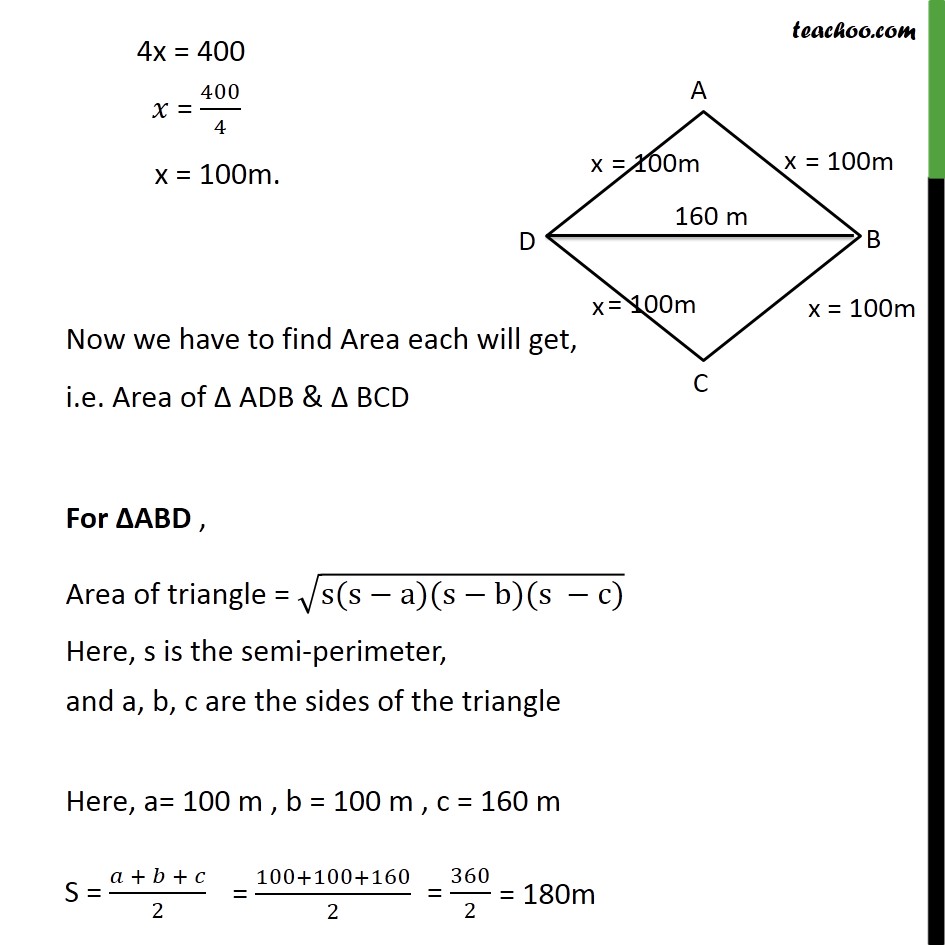
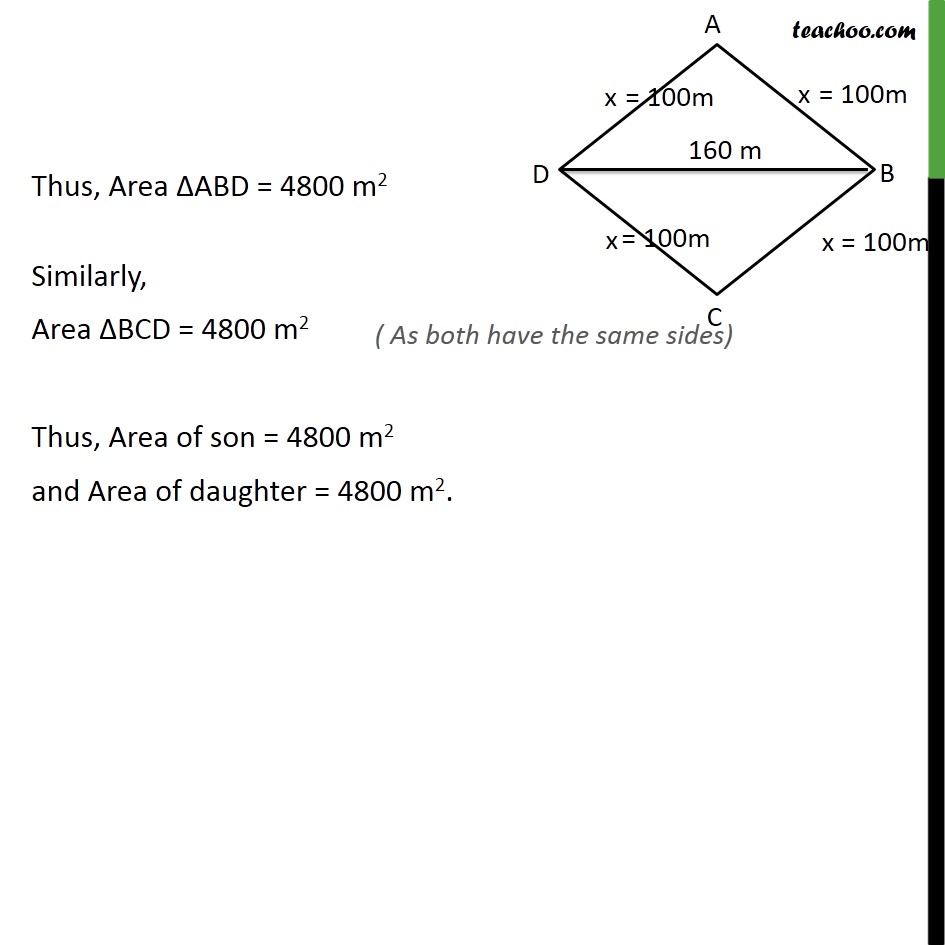
Question 3 Sanya has a piece of land which is in the shape of a rhombus She wants her one daughter and one son to work on the land and produce different crops. She divided the land in two equal parts. If the perimeter of the land is 400 m and one of the diagonals is 160 m, how much area each of them will get for their crops? Let the piece of land be ABCD It is Given that Diagonal = 160 m BD = 160 m. Also, Perimeter = 400 m AB + BC + CD + AD = 400 m 𝑥 + 𝑥 + 𝑥 + 𝑥 = 400 m 4x = 400 Now we have to find Area each will get, i.e. Area of Δ ADB & Δ BCD For ΔABD , Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Here, a= 100 m , b = 100 m , c = 160 m Area of Δ ABD =√(𝑠(𝑠 −𝑎)(𝑠 −𝑏)(𝑠 −𝑐)) Putting a= 100 m , b = 100 m , c = 160 m ,s = 180 m = √(180(180 −100)(180 −100)(180 −160)) = √(180×80×80×20) m2 = √((18×8×8×2)×(10)4) m2 = √(36×(8×8)×(10)4) = √(62×(82)×(10)4) = √((6)2) × √((82) ) × √((104) ) = 6 × 8 × 〖(104)〗^(1/2) = 6 × 8 × 102 = 6 × 8 × 100 = 4800 m2 Thus, Area ΔABD = 4800 m2 Similarly, Area ΔBCD = 4800 m2 Thus, Area of son = 4800 m2 and Area of daughter = 4800 m2.