Example 2 - Chapter 9 Class 9 Circles

Transcript

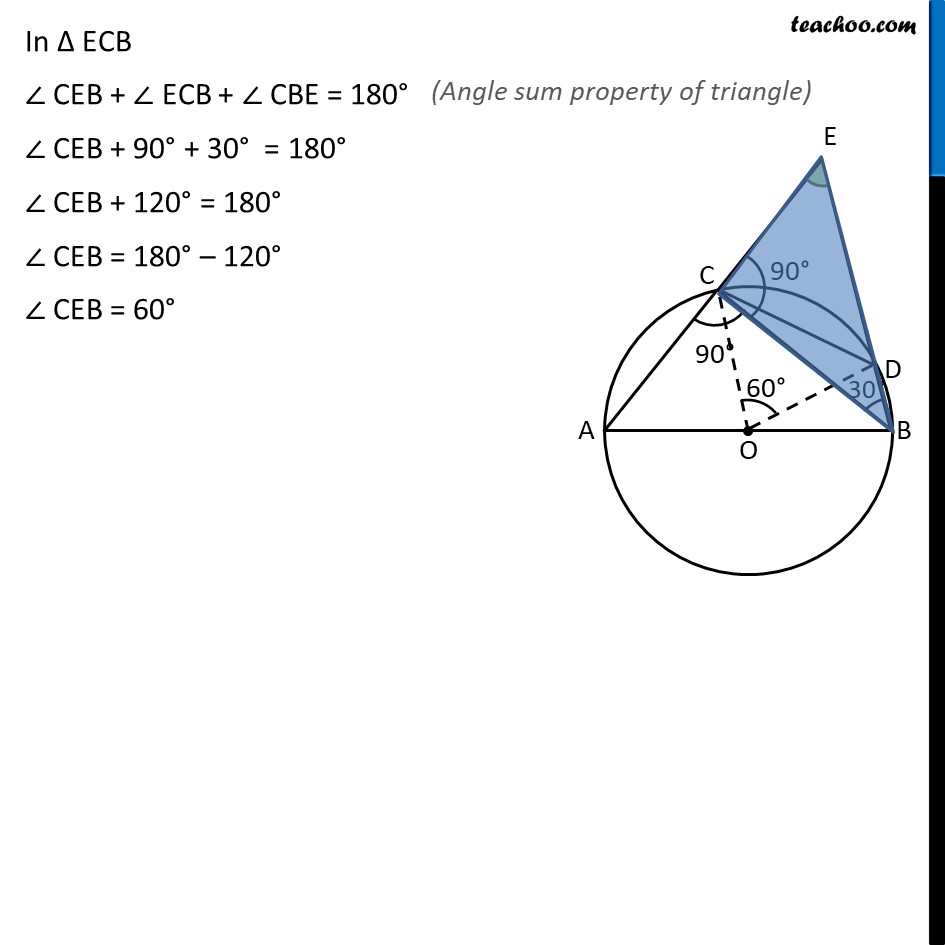
Example 2 In figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠ AEB = 60°. Given: AB is diameter of circle Chord CD, where CD = Radius of circle To prove: ∠AEB = 60° Construction: Join OC , OD & BC Proof: In Δ OCD OC = OD = CD = Radius of circle Since all sides are equal, Δ OCD is equilateral triangle ∠ COD = 60° Now, For arc CD subtends ∠ COD at centre & ∠ CBD at point B ∴ ∠ COD = 2 ∠ CBD 60° = 2∠ CBD 2∠ CBD = 60° ∠ CBD = (60°)/2 = 30° Now, Since AB is a diameter So, ∠ ACB = 90° Since AE is a line ∠ ACB + ∠ ECB = 180° 90° + ∠ ECB = 180° ∠ ECB = 180° – 90° = 90° In Δ ECB ∠ CEB + ∠ ECB + ∠ CBE = 180° ∠ CEB + 90° + 30° = 180° ∠ CEB + 120° = 180° ∠ CEB = 180° – 120° ∠ CEB = 60°