Ex 9.3, 3 - Chapter 9 Class 9 Circles

Last updated at July 26, 2026 by

Ex 9.3, 3 - In figure, ∠PQR = 100°, where P, Q and R - Ex 9.3 - Ex 9.3

part 2 - Ex 9.3, 3 - Ex 9.3 - Serial order wise - Chapter 9 Class 9 Circles

Remove Ads

Transcript

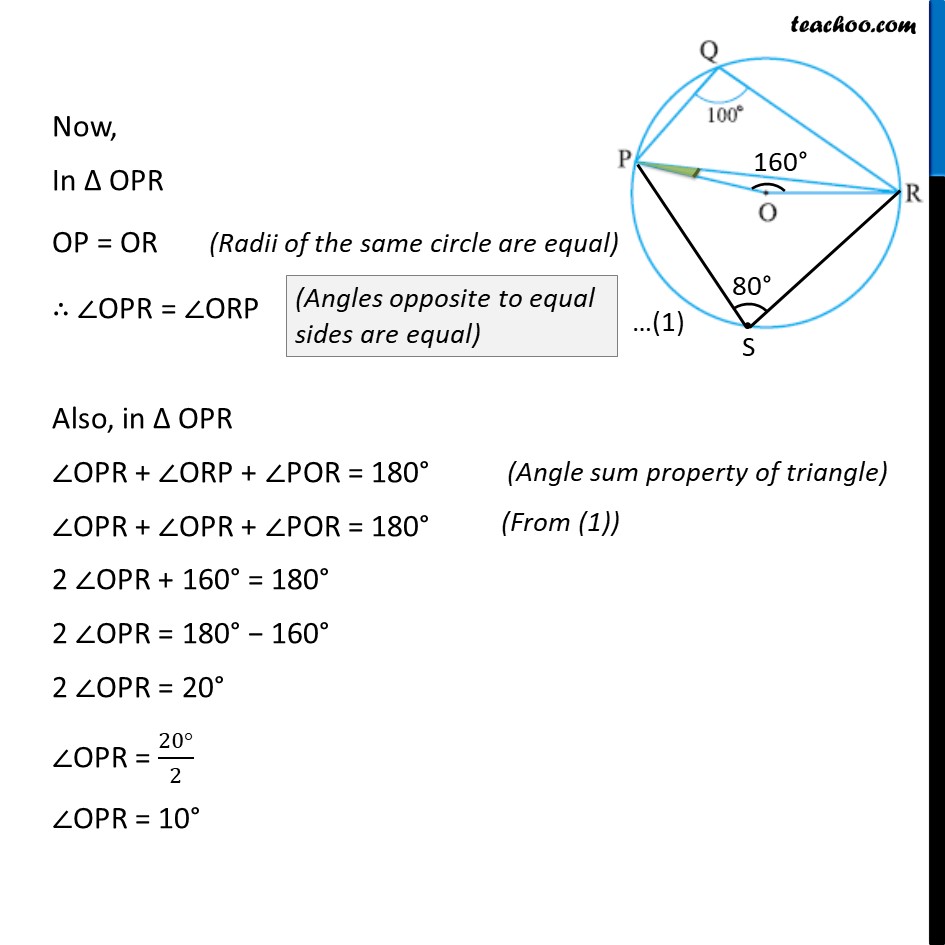
Ex 9.3, 3 In the given figure, PQR = 100 , where P, Q and R are points on a circle with centre O. Find OPR. Here, PR is chord We mark point S on the major arc of the circle. PQRS is a cyclic quadrilateral. So, PQR + PSR = 180 100 + PSR = 180 PSR = 180 100 PSR = 80 Arc PQR subtends POR at centre of circle. And PSR on point S So, POR = 2 PSR POR = 2 (80 ) = 160 Now, In OPR OP = OR OPR = ORP Also, in OPR OPR + ORP + POR = 180 OPR + OPR + POR = 180 2 OPR + 160 = 180 2 OPR = 180 160 2 OPR = 20 OPR = (20 )/2 OPR = 10

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.

Many students prefer Teachoo Black for a smooth, ad-free learning experience.