Ex 9.2, 1 - Chapter 9 Class 9 Circles

Transcript

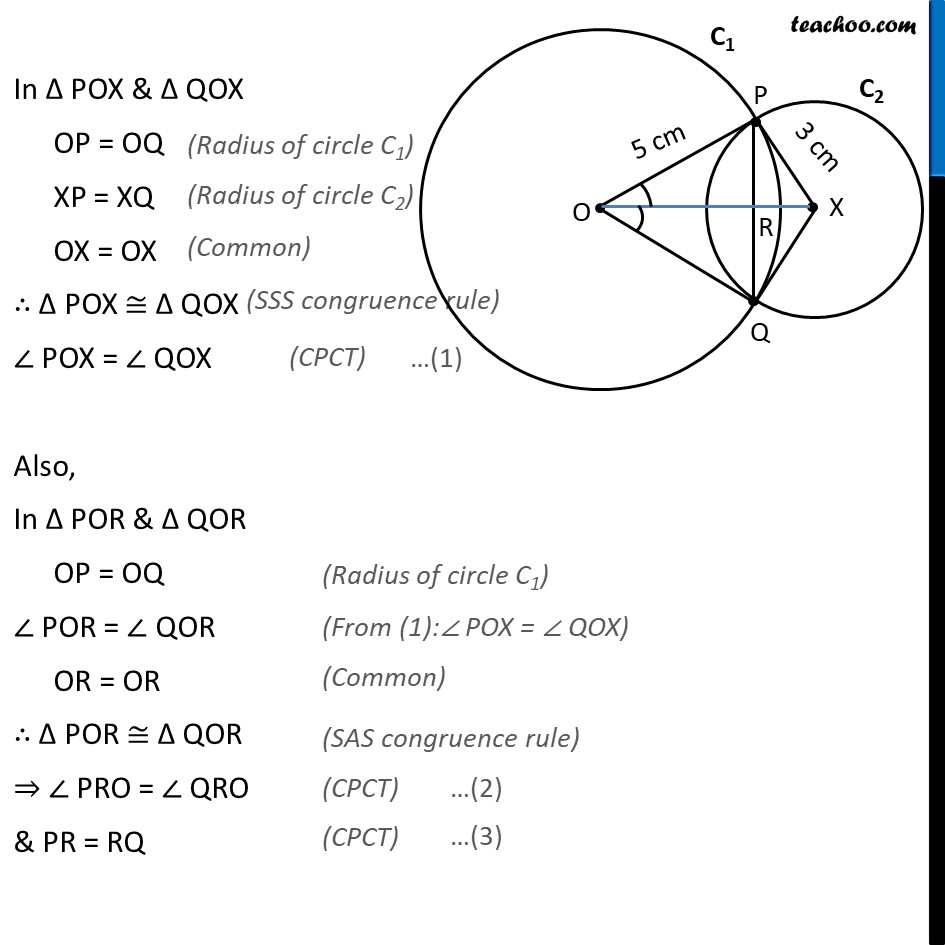
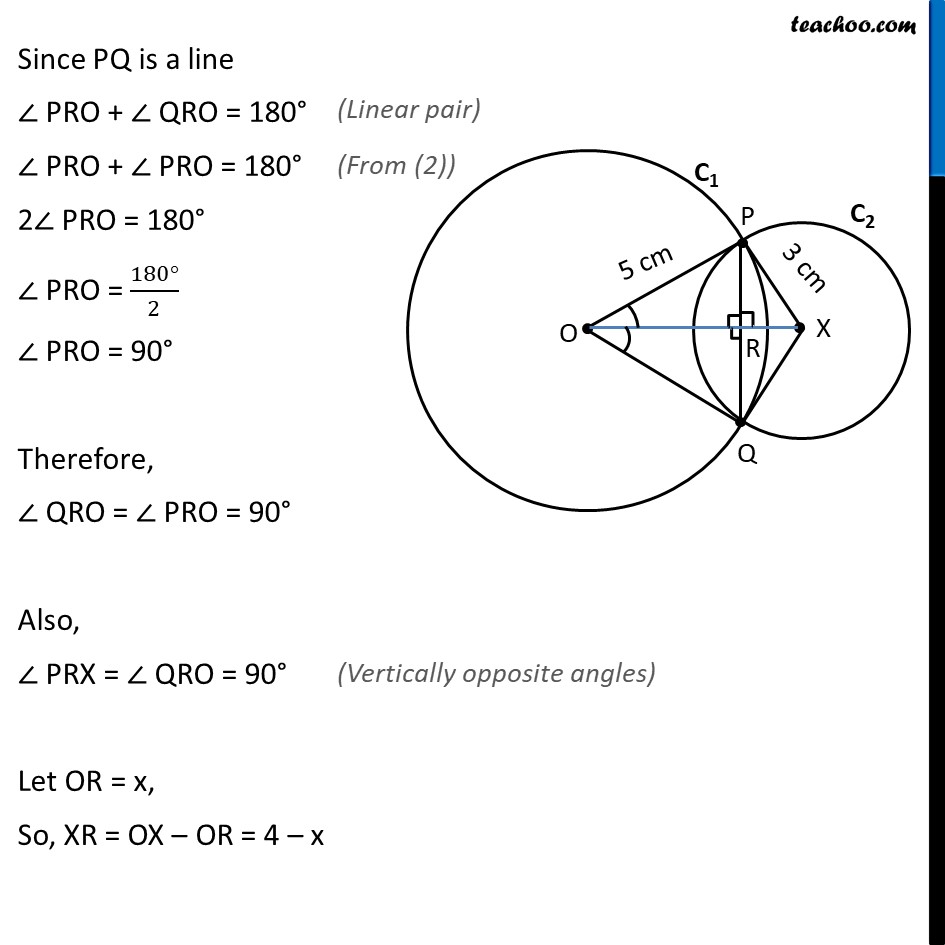
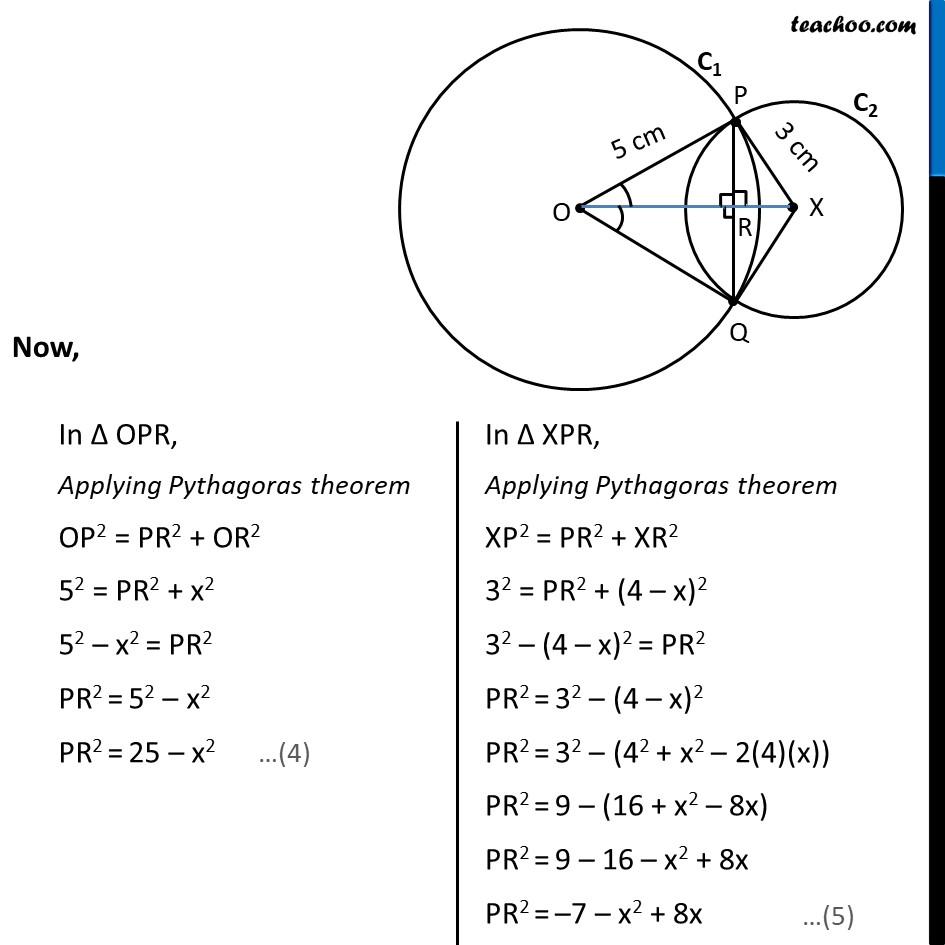
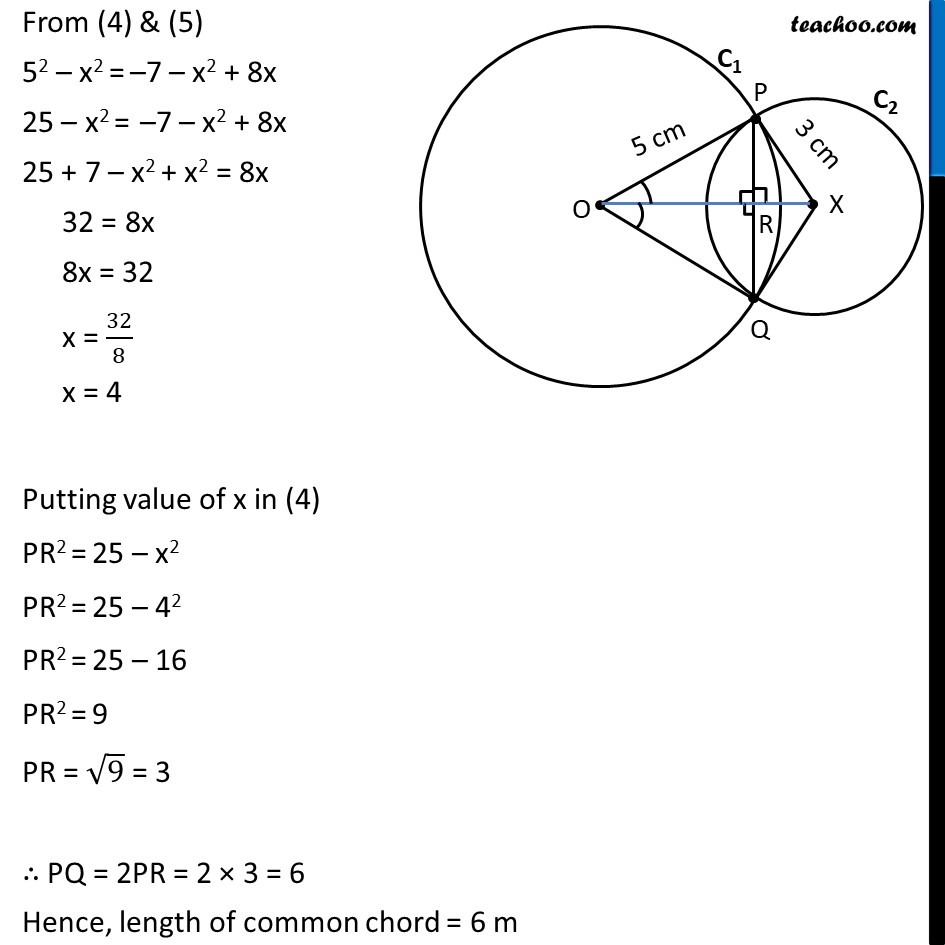
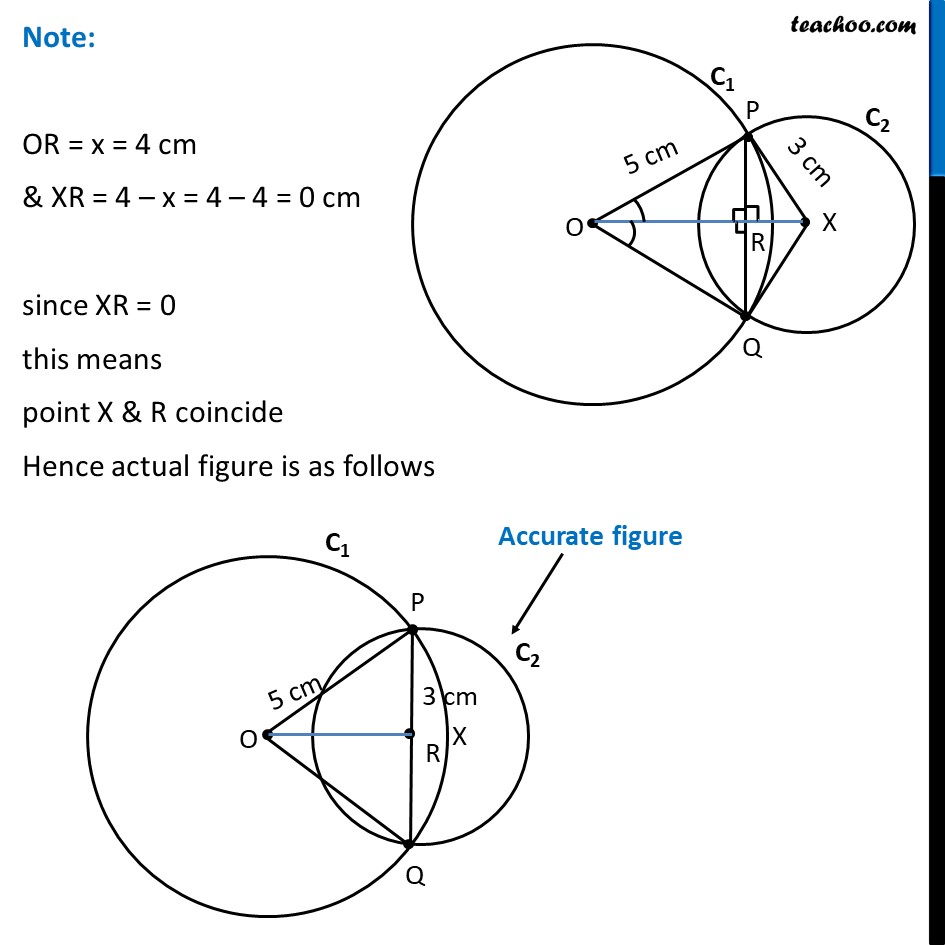
Ex 9.2, 1 Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord. Given: Circle C1 with radii 5cm & C2 with radii 3cm Intersecting at P & Q. OP = 5cm , XP = 3cm & OX = 4cm To find: Length of common chord i.e., length of PQ Solution: Let the point where OX intersects PQ be R. In Δ POX & Δ QOX OP = OQ XP = XQ OX = OX ∴ Δ POX ≅ Δ QOX ∠ POX = ∠ QOX Also, In Δ POR & Δ QOR OP = OQ ∠ POR = ∠ QOR OR = OR ∴ Δ POR ≅ Δ QOR ⇒ ∠ PRO = ∠ QRO & PR = RQ Since PQ is a line ∠ PRO + ∠ QRO = 180° ∠ PRO + ∠ PRO = 180° 2∠ PRO = 180° ∠ PRO = (180°)/2 ∠ PRO = 90° Therefore, ∠ QRO = ∠ PRO = 90° Also, ∠ PRX = ∠ QRO = 90° Let OR = x, So, XR = OX – OR = 4 – x Now, From (4) & (5) 52 – x2 = –7 – x2 + 8x 25 – x2 = –7 – x2 + 8x 25 + 7 – x2 + x2 = 8x 32 = 8x 8x = 32 x = 32/8 x = 4 Putting value of x in (4) PR2 = 25 – x2 PR2 = 25 – 42 PR2 = 25 – 16 PR2 = 9 PR = √9 = 3 ∴ PQ = 2PR = 2 × 3 = 6 Hence, length of common chord = 6 m Note: OR = x = 4 cm & XR = 4 – x = 4 – 4 = 0 cm since XR = 0 this means point X & R coincide Hence actual figure is as follows