Question 9 - Triangles with same base & same parallel lines - Areas of Parallelograms and Triangles

Transcript

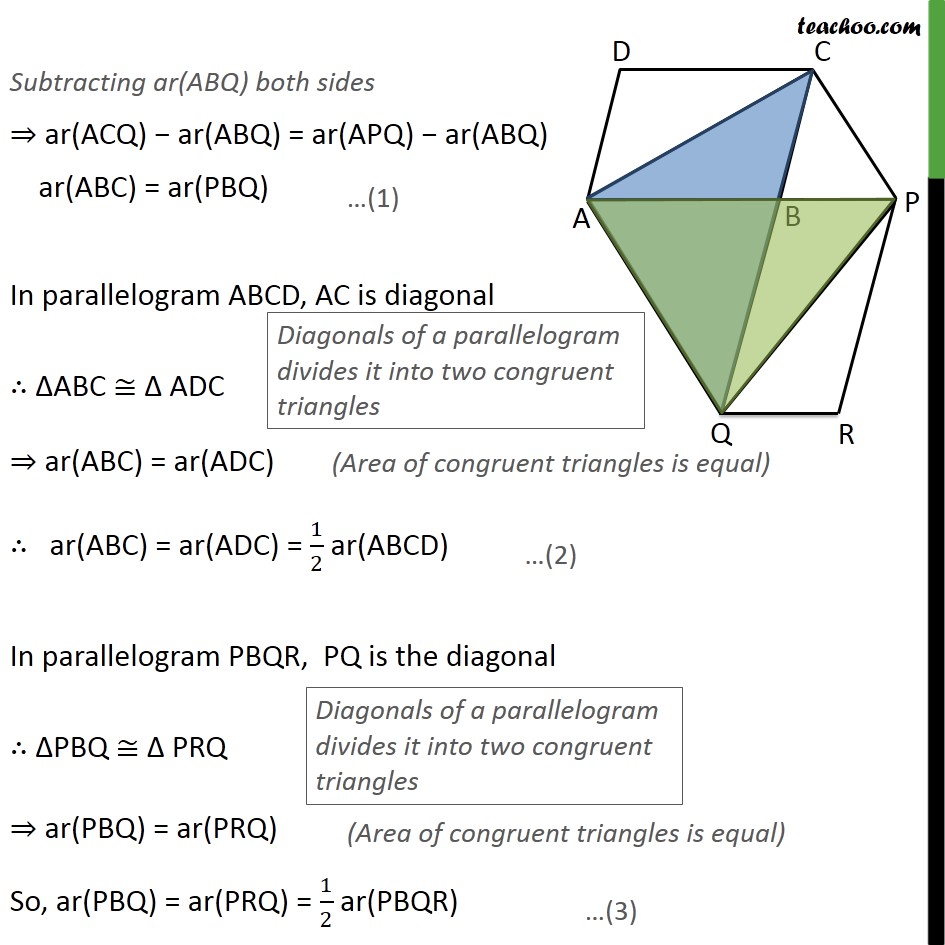
Question 9 The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that ar (ABCD) = ar (PBQR). Given: A parallelogram ABCD where CP AQ & PBQR is a parallelogram To prove: ar (ABCD) = ar (PBQR) Construction : Join AC & PQ Proof : For ACQ and AQP , ACQ and AQP are on the same base AQ and between the same parallels AQ and CP. ar(ACQ) = ar (APQ) Subtracting ar(ABQ) both sides ar(ACQ) ar(ABQ) = ar(APQ) ar(ABQ) ar(ABC) = ar(PBQ) In parallelogram ABCD, AC is diagonal ABC ADC ar(ABC) = ar(ADC) ar(ABC) = ar(ADC) = 1/2 ar(ABCD) In parallelogram PBQR, PQ is the diagonal PBQ PRQ ar(PBQ) = ar(PRQ) So, ar(PBQ) = ar(PRQ) = 1/2 ar(PBQR) From (1) ar(ABC) = ar(PBQ) 1/2 ar (ABCD) = 1/2 ar (PBQR) ar (ABCD) = ar (PBQR) Hence proved