Question 4 - Median divides triangle into two triangles of equal area - Areas of Parallelograms and Triangles

Transcript

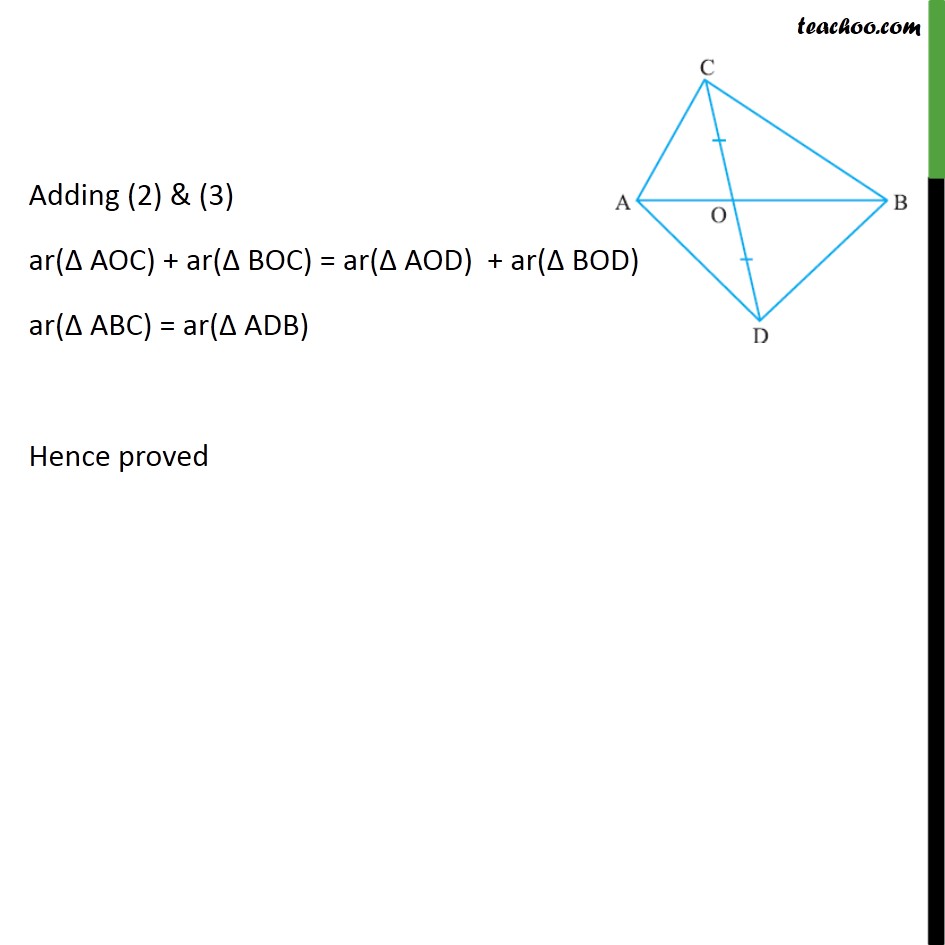
Question 4 In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD). Given: ΔABC and ΔABD on the same base AB & AB bisects CD, i.e. , OC = OD To prove: ar (ABC) = ar (ABD) Proof : In Δ ACD, Since OC = OD ∴ OA is the median. ⇒ ar(Δ AOC) = ar(Δ AOD) Similarly , in Δ BCD Since OC = OD ∴ OB is the median ⇒ ar(Δ BOC) = ar(Δ BOD) Adding (2) & (3) ar(Δ AOC) + ar(Δ BOC) = ar(Δ AOD) + ar(Δ BOD) ar(Δ ABC) = ar(Δ ADB) Hence proved