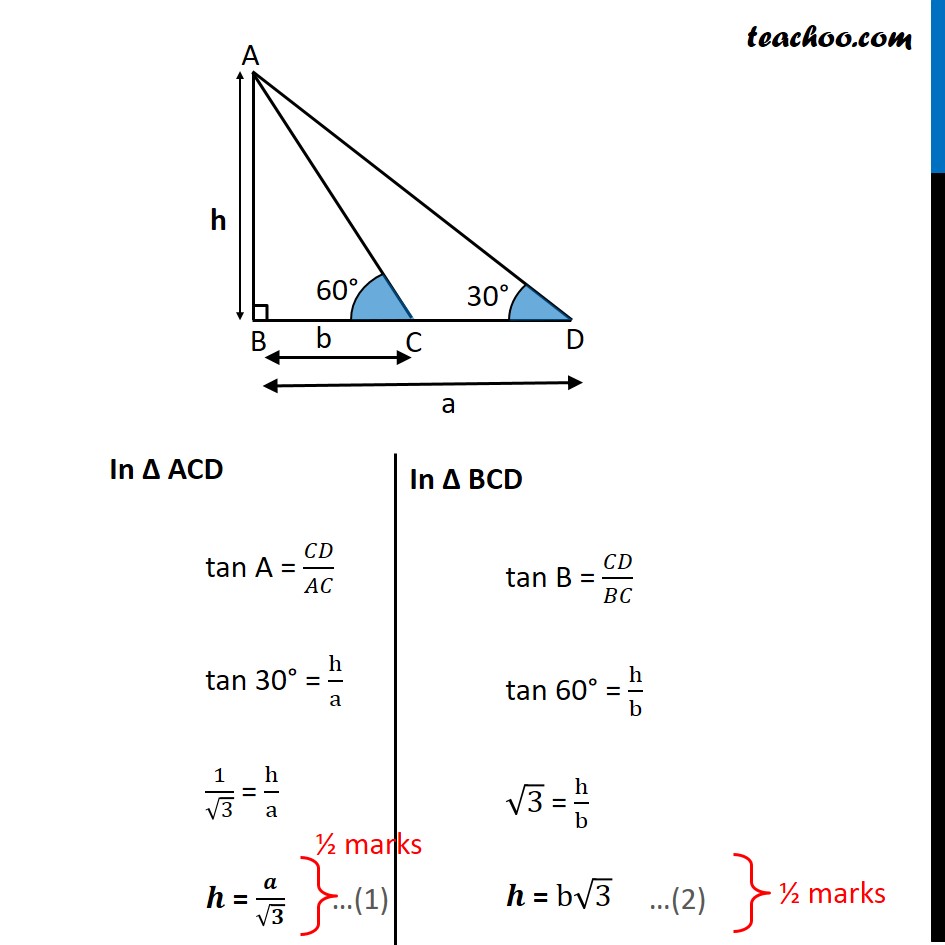
If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a > b) from its base and in the same straight line from it are 30° and 60° , then find the height of the candle.


CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard
CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard
Last updated at December 16, 2024 by Teachoo



Transcript
Question 32 If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a > b) from its base and in the same straight line from it are 30° and 60° , then find the height of the candle. Let AB be the candle and let the height of candle be ℎ cm Given BD = a and BC = b In Δ ACD tan A = 𝐶𝐷/𝐴𝐶 tan 30° = h/a 1/√3 = h/a 𝒉 = 𝒂/√𝟑 In Δ BCD tan B = 𝐶𝐷/𝐵𝐶 tan 60° = h/b √3 = h/b 𝒉 = b√3 Multiplying (1) and (2) ℎ × ℎ = 𝒂/√𝟑 × b√3 ℎ^2 = ab 𝒉 = √𝒂𝒃 cm Hence, Height of the Candle= √𝑎𝑏 cm