1. Class 10
  2. Solutions of Sample Papers for Class 10 Boards
  3. CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard

Question 28 (Choice - 1) - CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Last updated at Oct. 26, 2020 by

If one root of the quadratic equation 3x 2 + px + 4 = 0 is 2/3, then find
the value of p and the other root of the equation.

If one root of the quadratic equation 3x2+px+4=0 is 2/3, then find

Question 28 (Choice - 1) - CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard - Part 2
Question 28 (Choice - 1) - CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard - Part 3

  1. Class 10
  2. Solutions of Sample Papers for Class 10 Boards

    3. CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard

    CBSE Class 10 Sample Paper for 2021 Boards - Maths BasicΒ β†’

Transcript

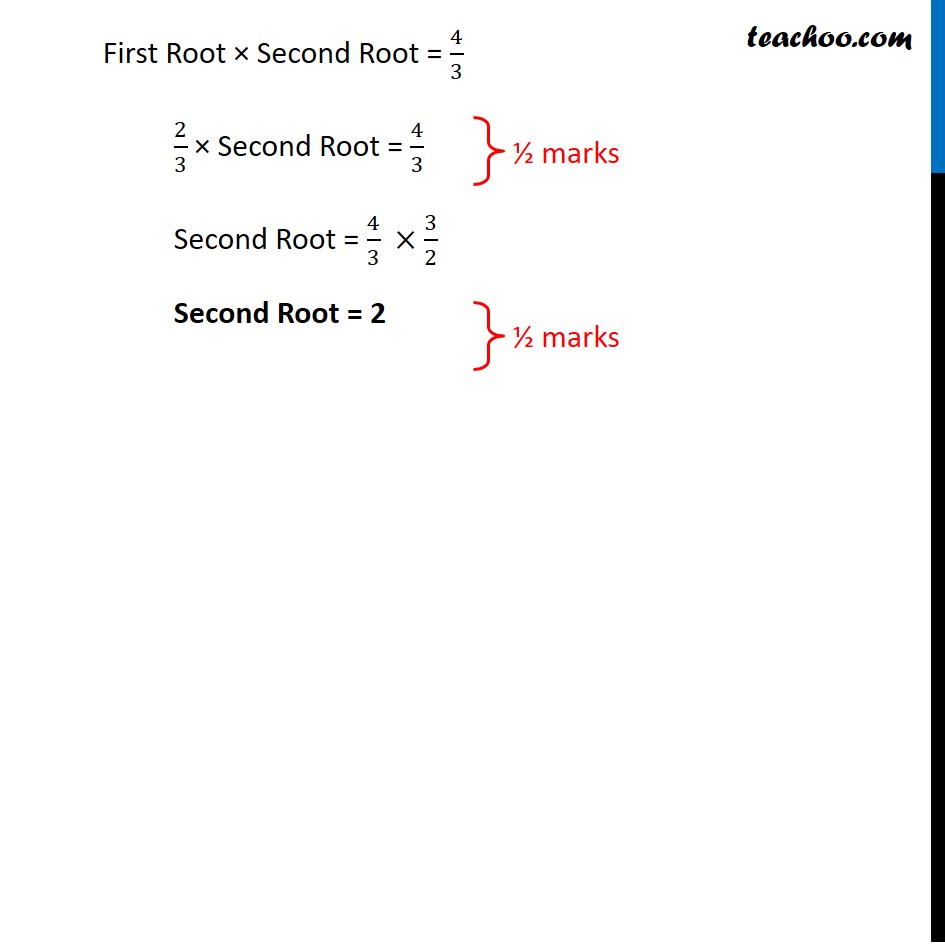
Question 28 (Choice - 1) If one root of the quadratic equation 3x2 + px + 4 = 0 is 2/3, then find the value of p and the other root of the equation.Since one root is 2/3 Putting 𝟐/πŸ‘ in equation 3x2 + px + 4 = 0 3(2/3)^2+𝑝 Γ—2/3+4=0 3 Γ—4/9+𝑝 Γ—2/3+4=0 4/3+𝑝 Γ—2/3+4=0 4/3+4+ 𝑝 Γ—2/3=0 (4 + 16)/3+ 𝑝 Γ—2/3=0 20/3+ 𝑝 Γ—2/3=0 𝑝 Γ—2/3=βˆ’20/3 𝑝 =βˆ’20/3 Γ—3/2 𝒑 = βˆ’10 Thus, our equation becomes 3x2 + px + 4 = 0 3x2 βˆ’ 10x + 4 = 0 Now, Product of Roots = πŸ’/πŸ‘ First Root Γ— Second Root = 4/3 2/3 Γ— Second Root = 4/3 Second Root = 4/3 Γ—3/2 Second Root = 2

Class 10
Solutions of Sample Papers for Class 10 Boards

About the Author

Davneet Singh's photo - Teacher, Engineer, Marketer
Davneet Singh
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur. He has been teaching from the past 10 years. He provides courses for Maths and Science at Teachoo.