
Last updated at December 13, 2024 by Teachoo


Transcript
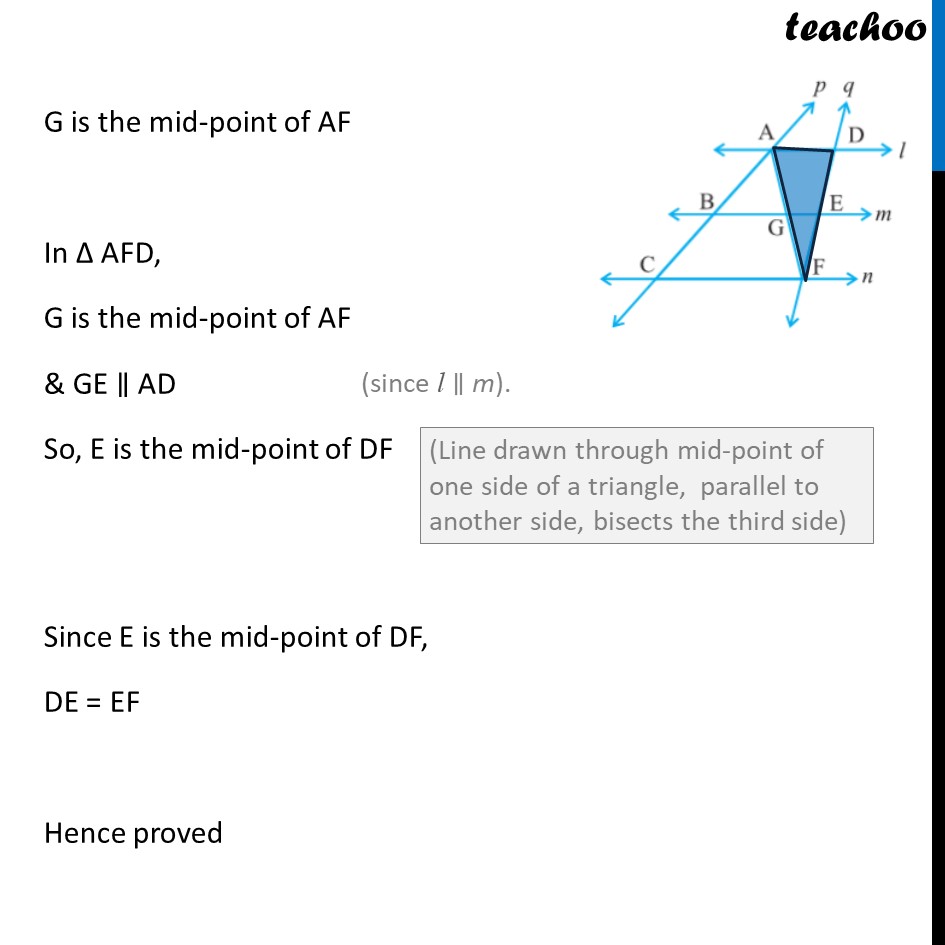
Example 7 l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p . Show that l, m and n cut off equal intercepts DE and EF on q also. Given: l m n l, m and n cut off equal intercepts AB and BC on p So, AB = BC To prove: l, m and n cut off equal intercepts DE and EF on q i.e. DE = EF Proof: Let us join A to F intersecting m at G.. In ACF, B is the mid-point of AC & BG CF So, G is the mid-point of AF In AFD, G is the mid-point of AF & GE AD So, E is the mid-point of DF Since E is the mid-point of DF, DE = EF Hence proved