
Last updated at Feb. 25, 2025 by Teachoo



Transcript
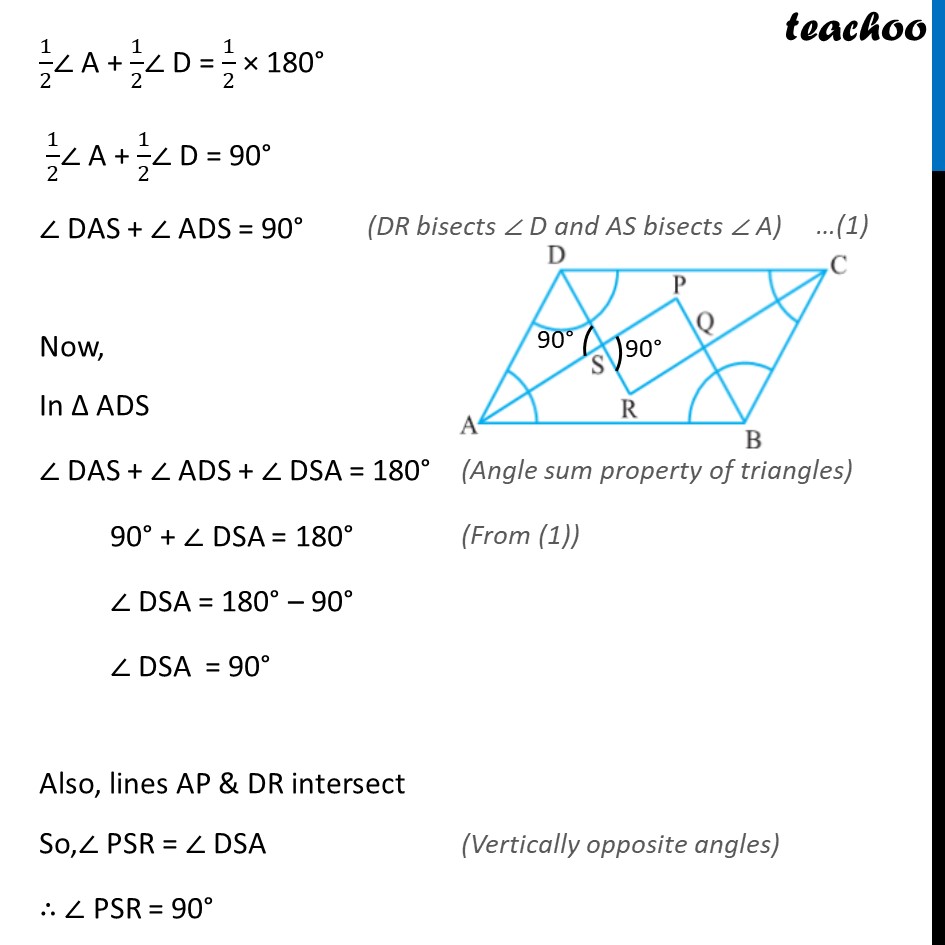
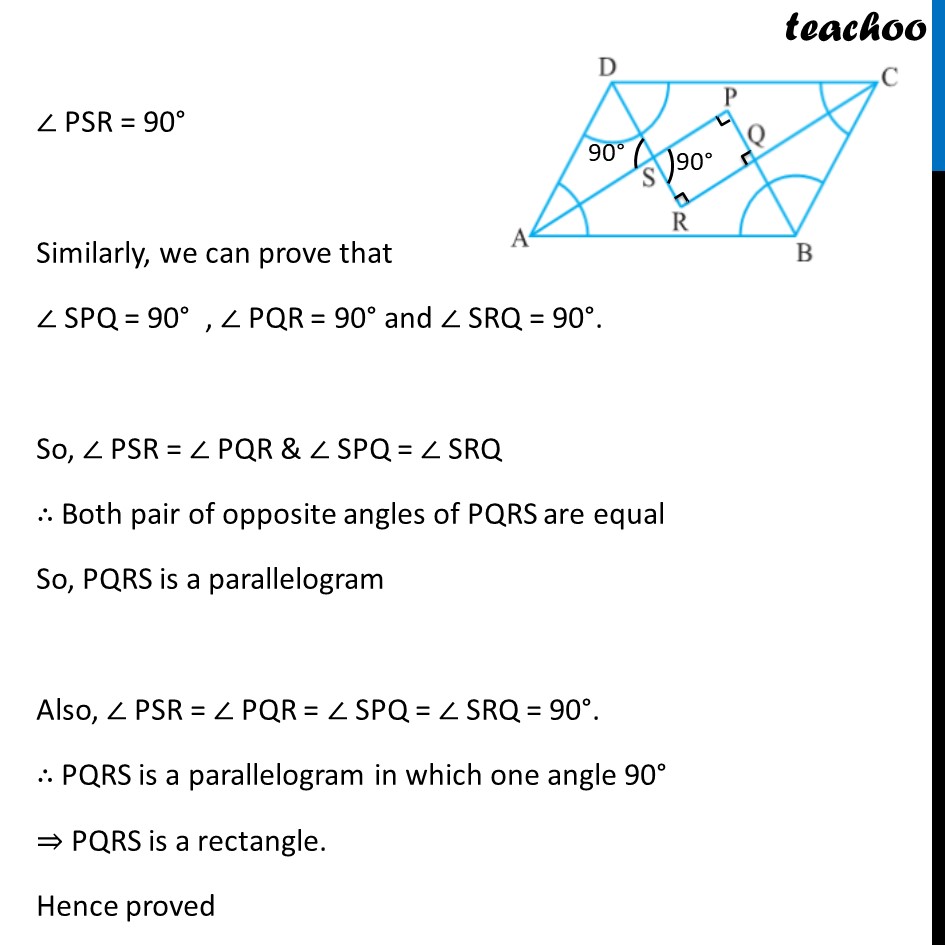
Example 5 Show that the bisectors of angles of a parallelogram form a rectangle. Given: ABCD is a parallelogram AP, BP, CR, DR are bisectors of ∠ A , ∠ B, ∠ C, ∠ D respectively To prove: PQRS is a rectangle Proof: A rectangle is a parallelogram with one angle 90° First we will prove PQRS is a parallelogram Now, AB ∥ DC & AD is transversal ∴ ∠ A + ∠ D = 180° Multiplying by half 1/2∠ A + 1/2∠ D = 1/2 × 180° 1/2∠ A + 1/2∠ D = 90° ∠ DAS + ∠ ADS = 90° Now, In Δ ADS ∠ DAS + ∠ ADS + ∠ DSA = 180° 90° + ∠ DSA = 180° ∠ DSA = 180° – 90° ∠ DSA = 90° Also, lines AP & DR intersect So,∠ PSR = ∠ DSA ∴ ∠ PSR = 90° Similarly, we can prove that ∠ SPQ = 90° , ∠ PQR = 90° and ∠ SRQ = 90°. So, ∠ PSR = ∠ PQR & ∠ SPQ = ∠ SRQ ∴ Both pair of opposite angles of PQRS are equal So, PQRS is a parallelogram Also, ∠ PSR = ∠ PQR = ∠ SPQ = ∠ SRQ = 90°. ∴ PQRS is a parallelogram in which one angle 90° ⇒ PQRS is a rectangle. Hence proved