Example 3 - Chapter 8 Class 9 Quadrilaterals

Transcript

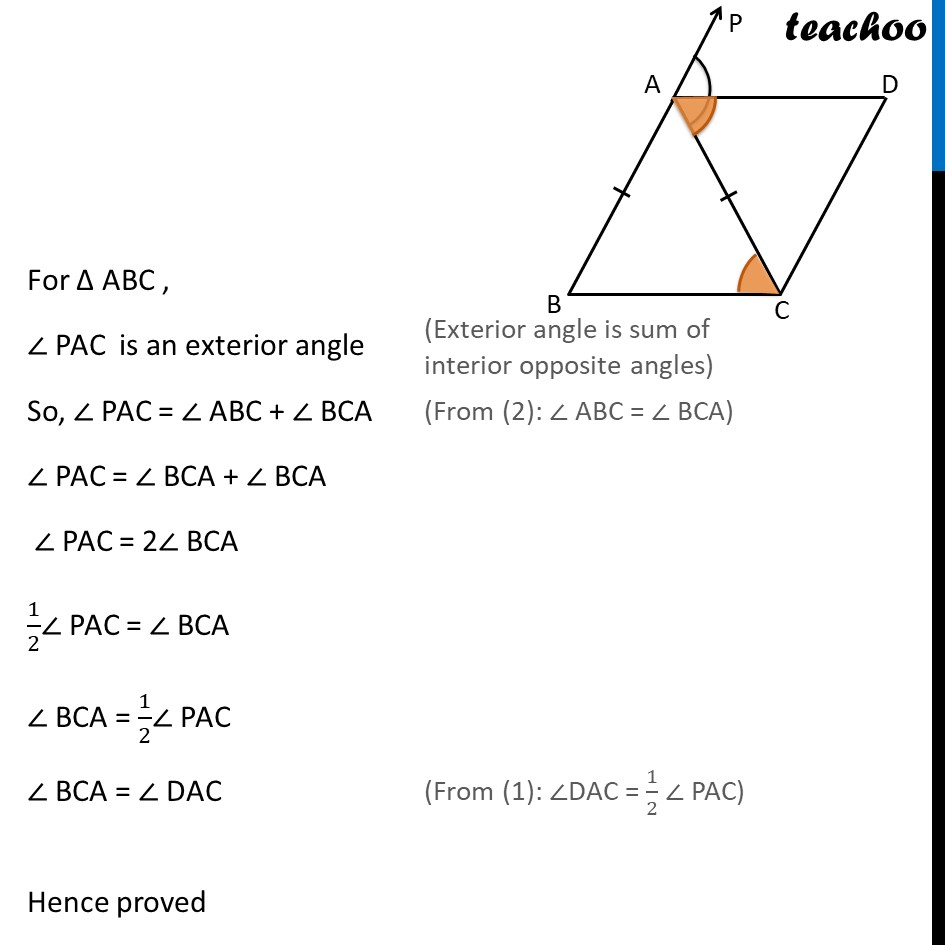
Example 3 ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD AB. Show that DAC = BCA and Given: ABC where AB = AC AD bisects PAC, & CD AB To prove: DAC = BCA Proof: AD bisects PAC Hence PAD = DAC = 1/2 PAC Also, given AB = AC BCA = ABC For ABC , PAC is an exterior angle So, PAC = ABC + BCA PAC = BCA + BCA PAC = 2 BCA 1/2 PAC = BCA BCA = 1/2 PAC BCA = DAC Hence proved Example 3 ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD AB .Show that (ii) ABCD is a parallelogram. In previous part we proved , DAC = BCA For lines BC , AD with transversal AC DAC & BCA are alternate interior angles and they are equal So, BC AD Now, In ABCD BC AD & AB CD Since both pairs of opposite sides of quadrilateral ABCD are parallel. ABCD is a parallelogram.