Ex 8.2, 3 - Chapter 8 Class 9 Quadrilaterals

Transcript

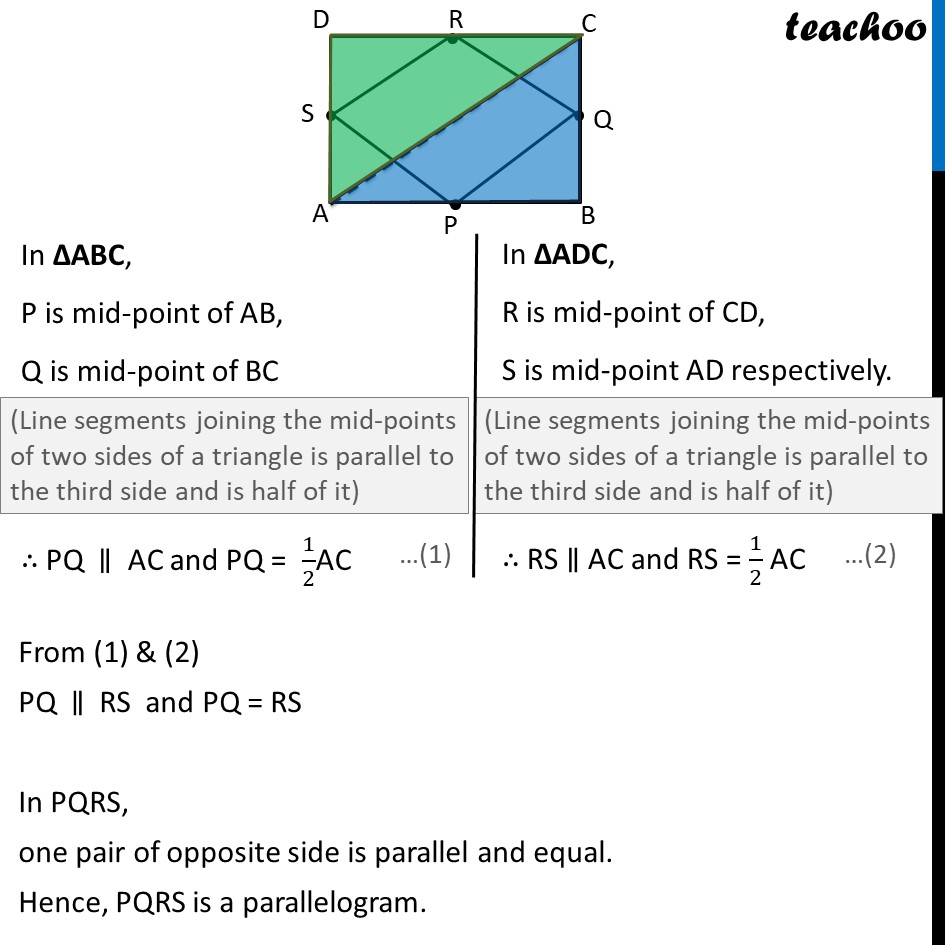
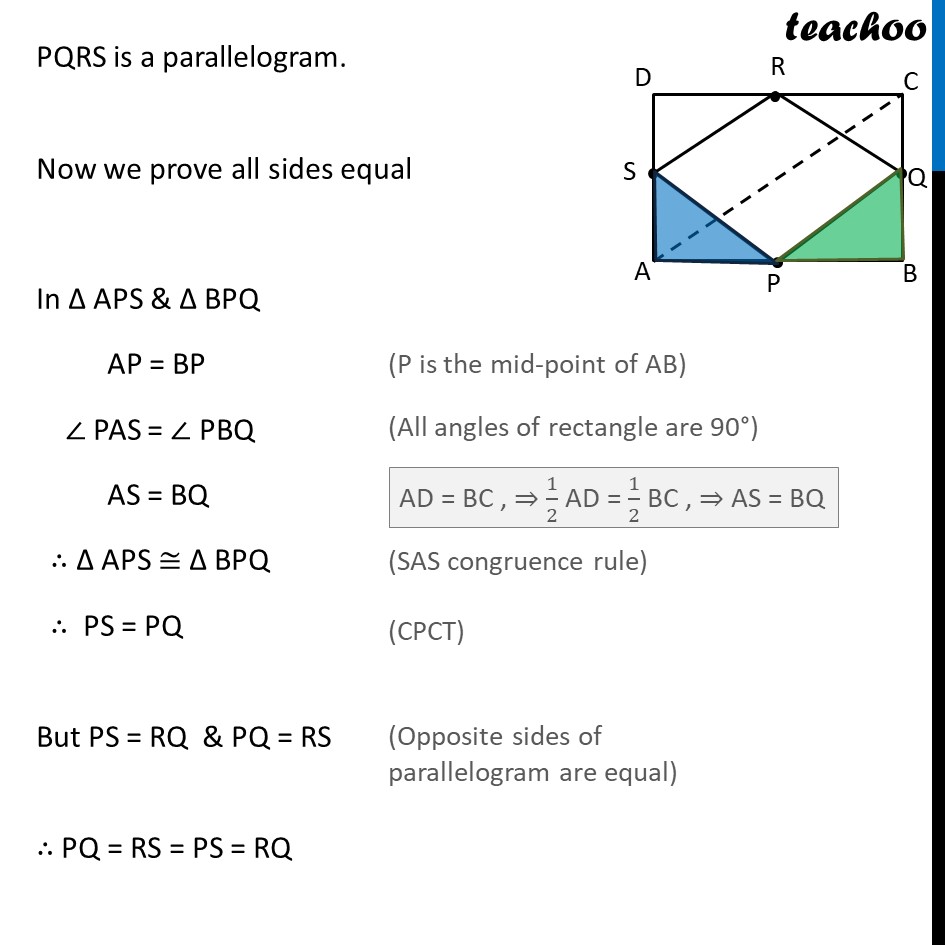
Ex .8.2, 3 ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus. Given: ABCD is rectangle where P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively To prove: PQRS is a rhombus Construction: Join A & C Proof: A rhombus is a parallelogram with all sides equal First we will prove PQRS is a parallelogram, and then prove all sides equal From (1) & (2) PQ ∥ RS and PQ = RS In PQRS, one pair of opposite side is parallel and equal. Hence, PQRS is a parallelogram. Now we prove all sides equal In ∆ APS & ∆ BPQ AP = BP ∠ PAS = ∠ PBQ AS = BQ ∴ ∆ APS ≅ ∆ BPQ ∴ PS = PQ But PS = RQ & PQ = RS ∴ PQ = RS = PS = RQ Hence, all sides are equal Thus, PQRS is a parallelogram with all sides equal So, PQRS is a rhombus Hence proved