Question 3 - Diagonal of parallelogram - Chapter 8 Class 9 Quadrilaterals

Transcript

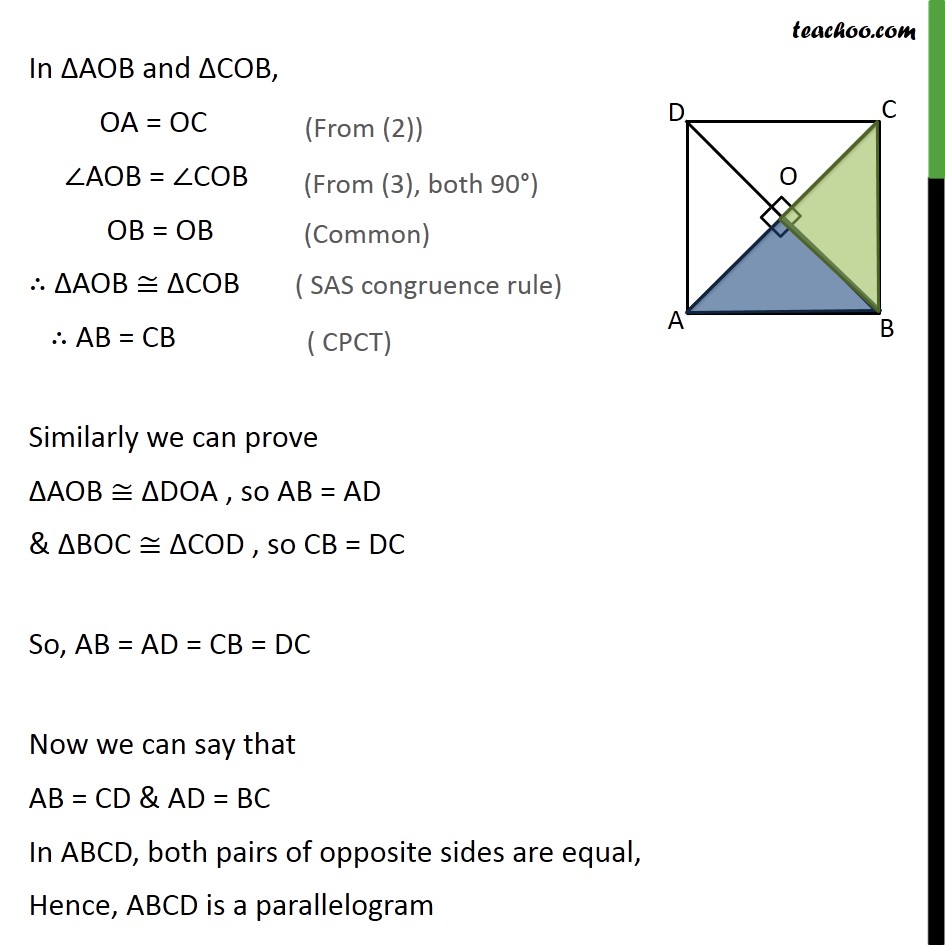
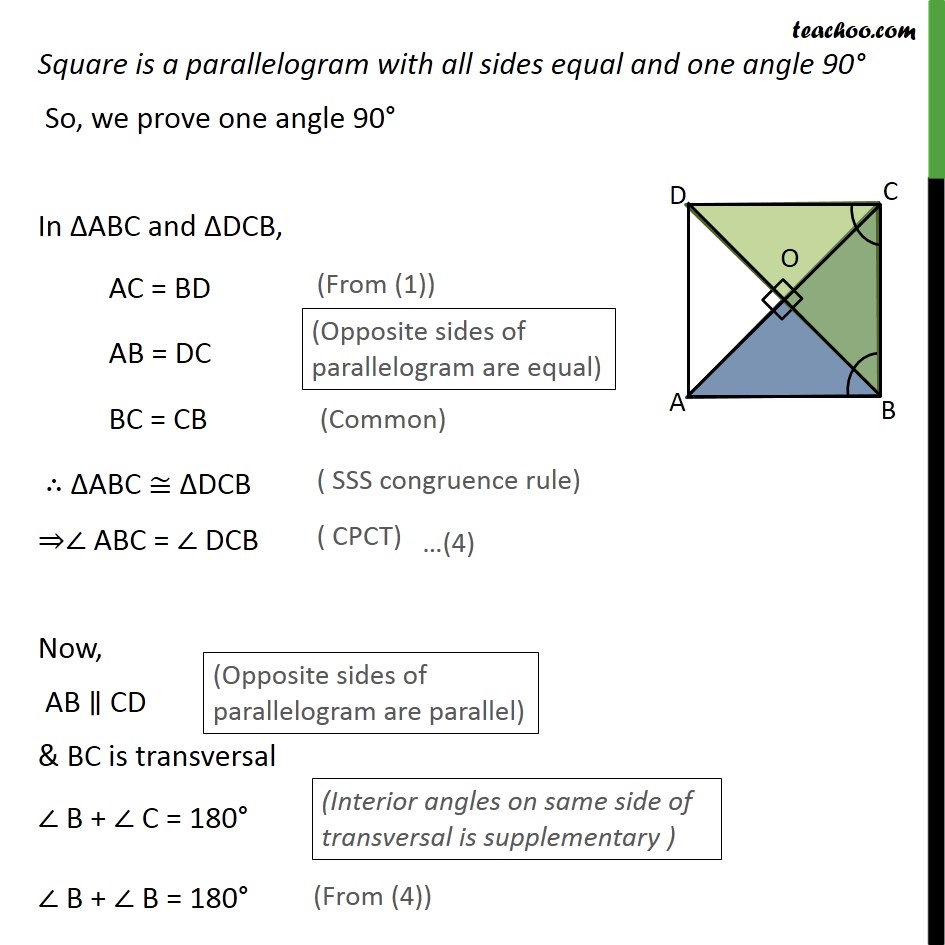
Ex 8.1, 5 Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square. Given: Let ABCD be the quadrilateral. Diagonals are equal, i.e., AC = BD & bisect each other, i.e. OA = OC & OB = OD, at right angles ,i.e., ∠AOB = ∠BOC = ∠COD = ∠AOD = 90° To prove: ABCD is a square Proof: Square is a parallelogram with all sides equal and one angle 90° First we will prove ABCD is a parallelogram and then prove all sides equal , and one angle equal to 90° In ΔAOB and ΔCOB, OA = OC ∠AOB = ∠COB OB = OB ∴ ΔAOB ≅ ΔCOB ∴ AB = CB Similarly we can prove ΔAOB ≅ ΔDOA , so AB = AD & ΔBOC ≅ ΔCOD , so CB = DC So, AB = AD = CB = DC Now we can say that AB = CD & AD = BC In ABCD, both pairs of opposite sides are equal, Hence, ABCD is a parallelogram Square is a parallelogram with all sides equal and one angle 90° So, we prove one angle 90° In ΔABC and ΔDCB, AC = BD AB = DC BC = CB ∴ ΔABC ≅ ΔDCB ⇒∠ ABC = ∠ DCB Now, AB ∥ CD & BC is transversal ∠ B + ∠ C = 180° ∠ B + ∠ B = 180° 2∠ B = 180° ∠ B = (180°)/2 = 90° Thus, ABCD is a parallelogram with all sides equal and one angle 90° So, ABCD is a square