Ex 8.1, 2 - Chapter 8 Class 9 Quadrilaterals

Transcript

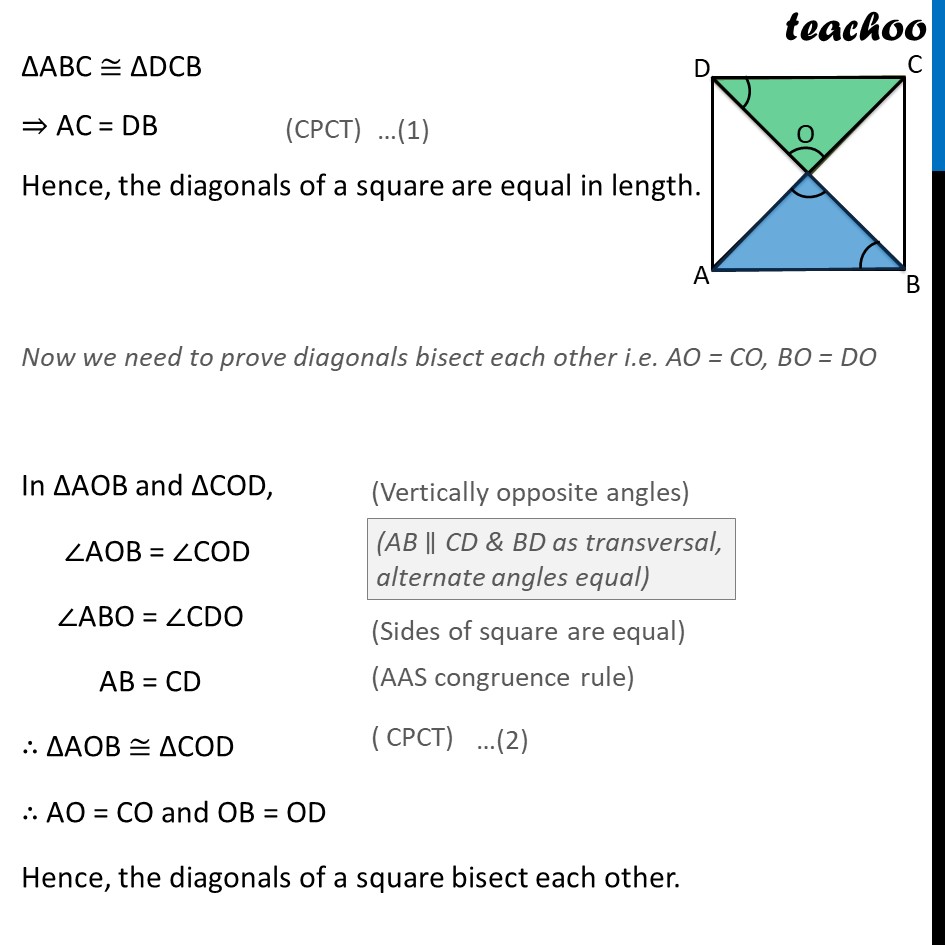
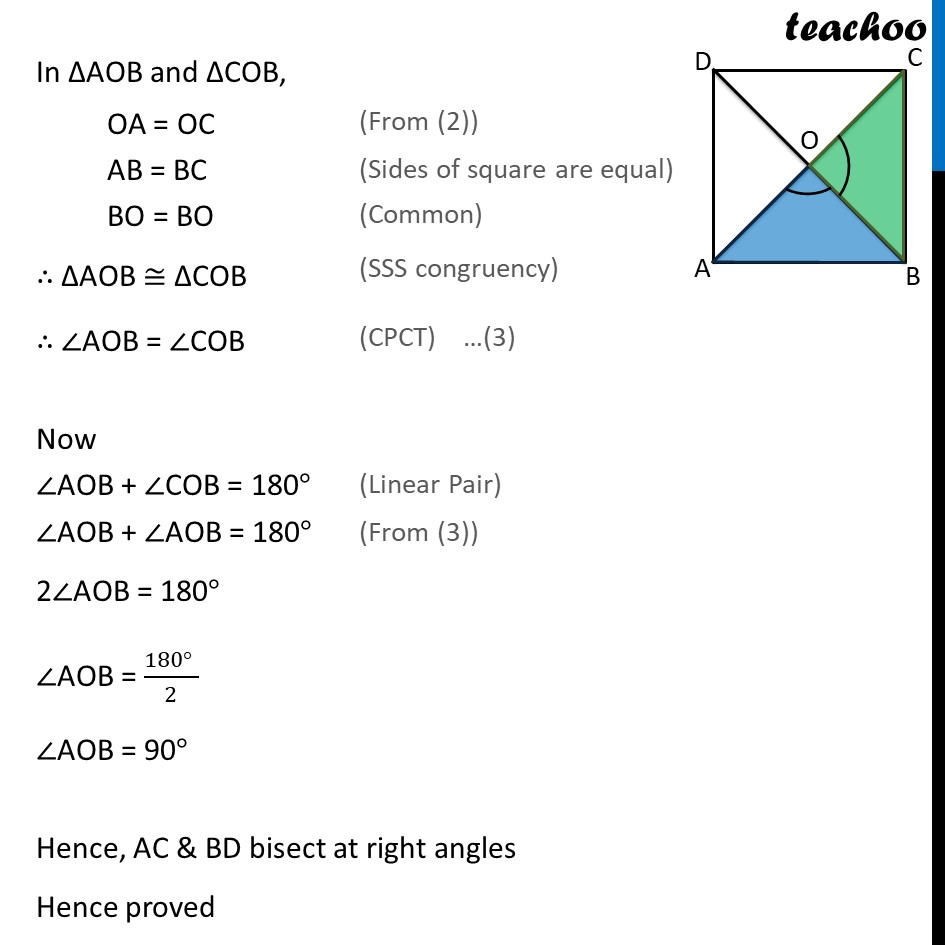
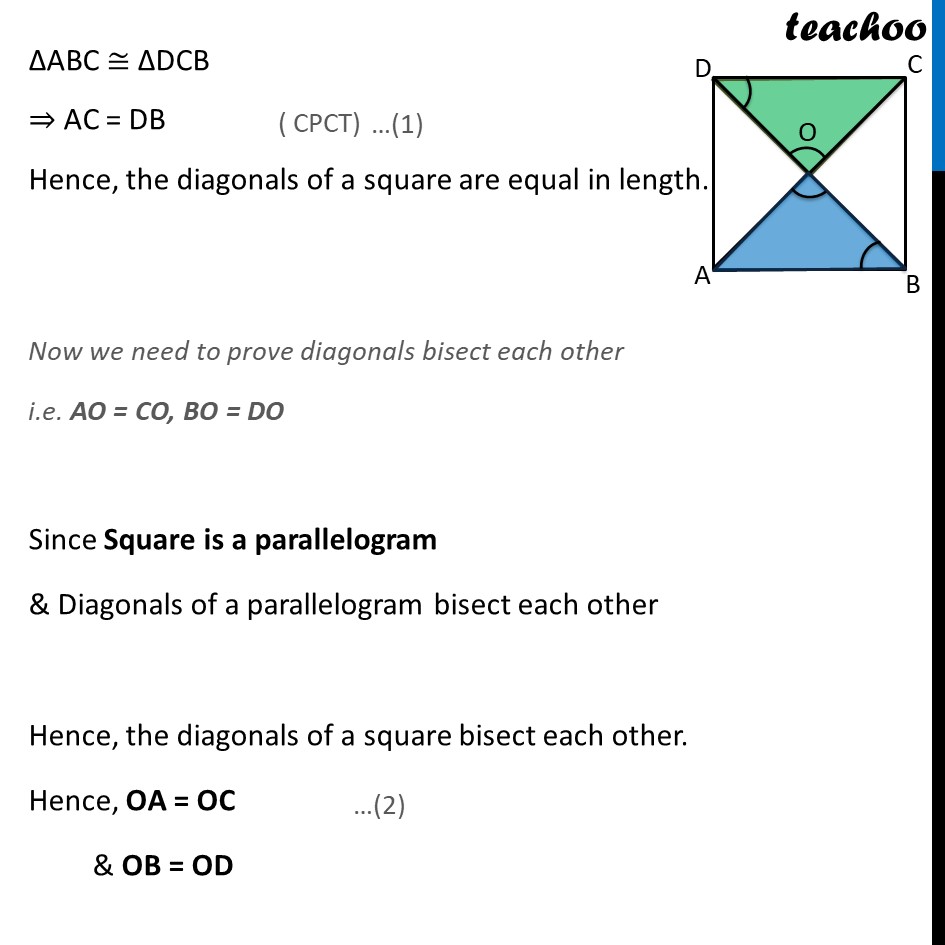
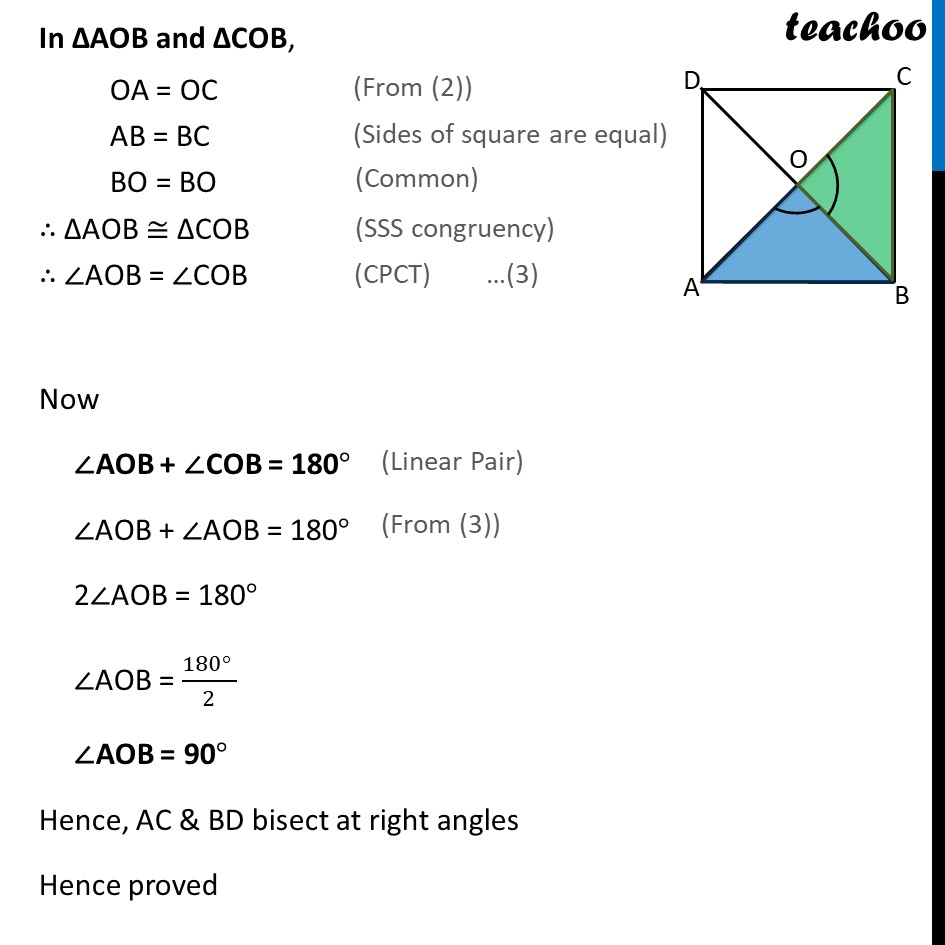
Ex 8.1, 4 Show that the diagonals of a square are equal and bisect each other at right angles. Given: ABCD be a square. Diagonals intersect at O. To prove : We need to prove 3 things 1. The diagonals of a square are equal ,i.e. AC = BD 2. bisect each other, i.e. OA = OC & OB = OD, 3. at right angles ,any of AOB , BOC , COD , AOD is 90 Proof: In ABC and DCB, AB = DC ABC = DCB BC = BC ABC DCB AC = DB Hence, the diagonals of a square are equal in length. Now we need to prove diagonals bisect each other i.e. AO = CO, BO = DO In AOB and COD, AOB = COD ABO = CDO AB = CD AOB COD AO = CO and OB = OD Hence, the diagonals of a square bisect each other. In AOB and COB, OA = OC AB = BC BO = BO AOB COB AOB = COB Now AOB + COB = 180 AOB + AOB = 180 2 AOB = 180 AOB = (180 )/2 AOB = 90 Hence, AC & BD bisect at right angles Hence proved Ex 8.1, 4 (Method 2) Show that the diagonals of a square are equal and bisect each other at right angles. Ex 8.1, 4 (Method 2) Show that the diagonals of a square are equal and bisect each other at right angles. Given: ABCD be a square. Diagonals intersect at O. To prove: We need to prove 3 things The diagonals of a square are equal ,i.e. AC = BD Bisect each other, i.e. OA = OC & OB = OD At right angles, any of ∠AOB , ∠BOC , ∠COD , ∠AOD is 90° Proof: In ΔABC and ΔDCB, AB = DC ∠ABC = ∠DCB BC = CB ∴ ΔABC ≅ ΔDCB Therefore AC = DB Hence, the diagonals of a square are equal in length (Sides of square are equal) (Both 90° , as all angles of square are 90°) (Common) ( SAS congruence rule) ( CPCT) …(1) Now we need to prove diagonals bisect each other i.e. AO = CO, BO = DO Since Square is a parallelogram & Diagonals of a parallelogram bisect each other Hence, the diagonals of a square bisect each other. i.e., OA = OC & OB = OD Now, we have to prove diagonals bisect each other at right angles In ΔAOB and ΔCOB, OA = OC AB = CB BO = BO ∴ ΔAOB ≅ ΔCOB Therefore ∠AOB = ∠COB Now ∠AOB + ∠COB = 180° ∠AOB + ∠AOB = 180° 2∠AOB = 180° (From (2)) (Sides of square are equal) (Common) (SSS congruency) (CPCT) (Linear Pair) (From (3)) ∠AOB = (180° )/2 ∠AOB = 90° Therefore, AC & BD bisect at right angles Hence proved