Example 6 - Chapter 7 Class 9 Triangles (Important Question)

Last updated at Dec. 13, 2024 by

Slide12.JPG

Slide13.JPG

Go Ad-free

Transcript

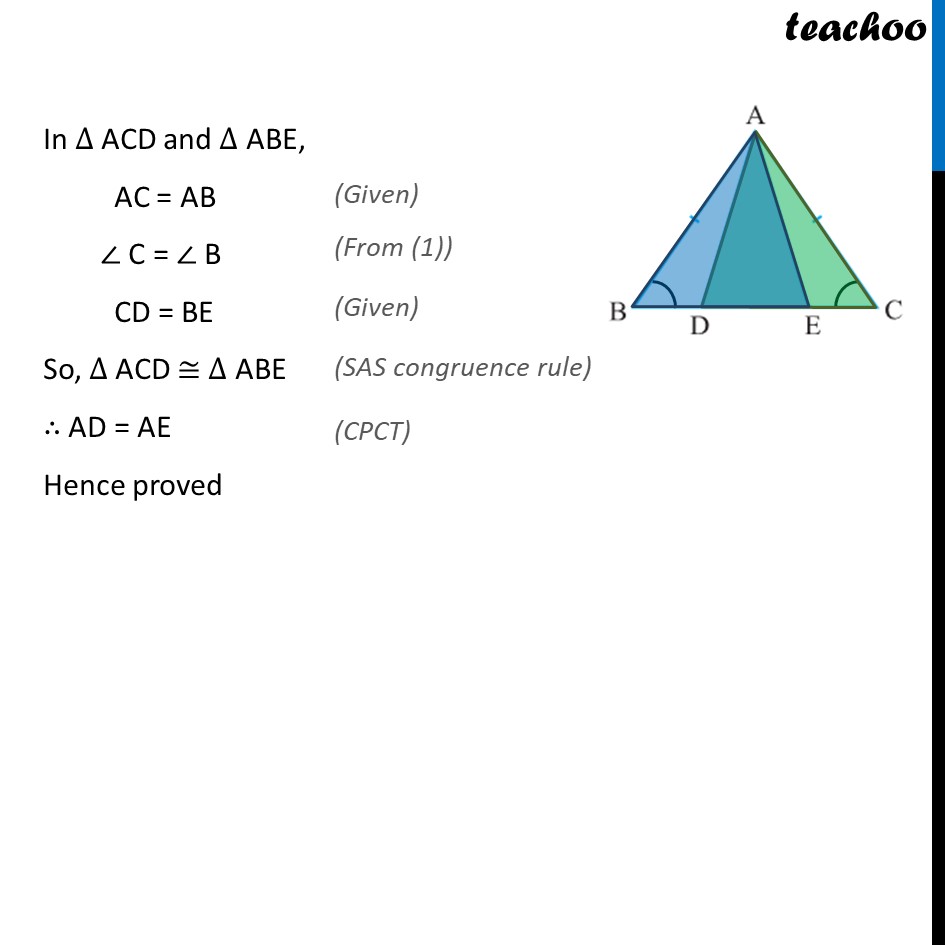
Example 6 In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see figure). Show that AD = AE. Given: ∆ ABC is isosceles, So, AB = AC Also, BE = CD To prove: AD = AE Proof: Since AB = AC Therefore, ∠ C = ∠ B In ∆ ACD and ∆ ABE, AC = AB ∠ C = ∠ B CD = BE So, ∆ ACD ≅ ∆ ABE ∴ AD = AE Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo