
Last updated at Dec. 13, 2024 by Teachoo


Transcript
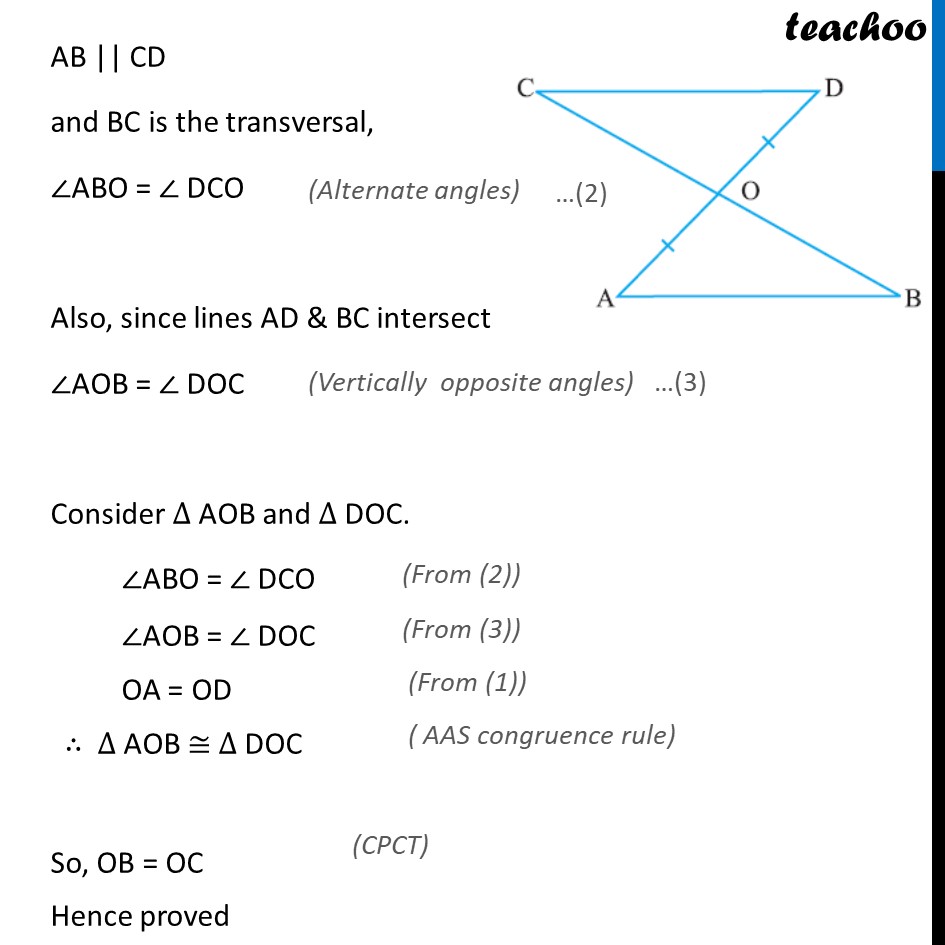
Example 3 Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC Given: AB || CD O is the mid-point of AD i.e. OA = OD To prove: (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC i.e. OB = OC Proof: AB || CD and BC is the transversal, ∠ABO = ∠ DCO Also, since lines AD & BC intersect ∠AOB = ∠ DOC Consider ∆ AOB and ∆ DOC. ∠ABO = ∠ DCO ∠AOB = ∠ DOC OA = OD ∴ ∆ AOB ≅ ∆ DOC So, OB = OC Hence proved