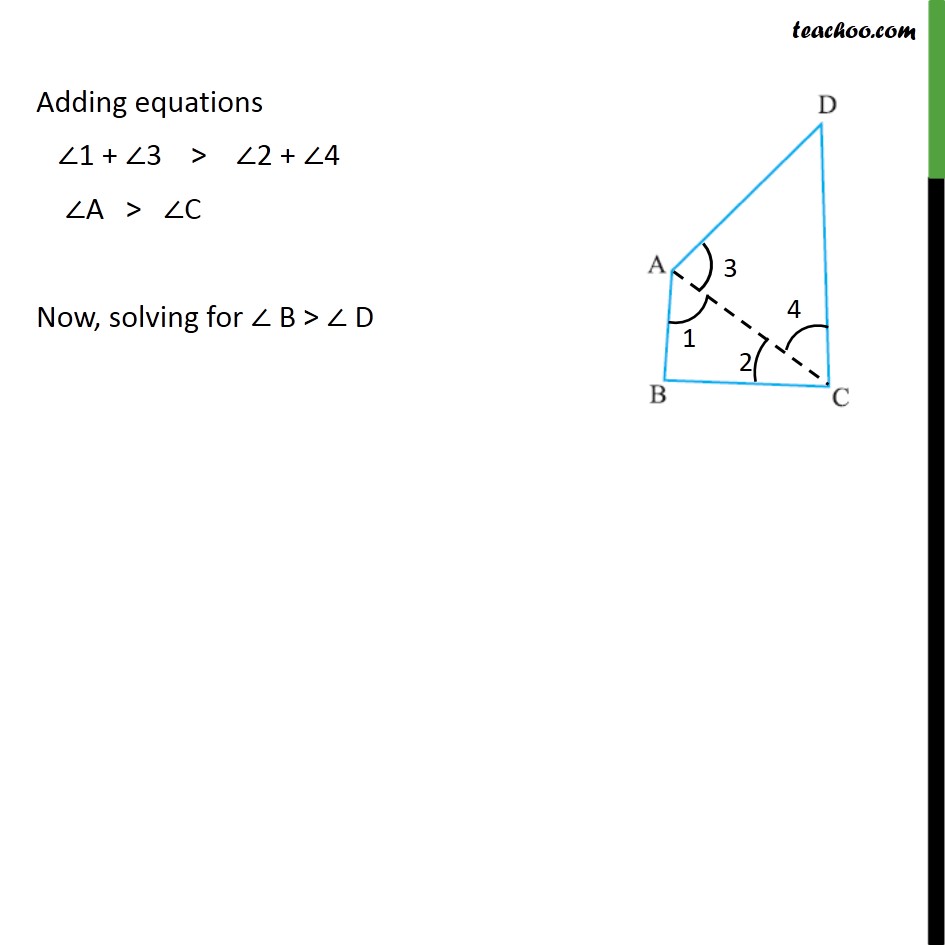
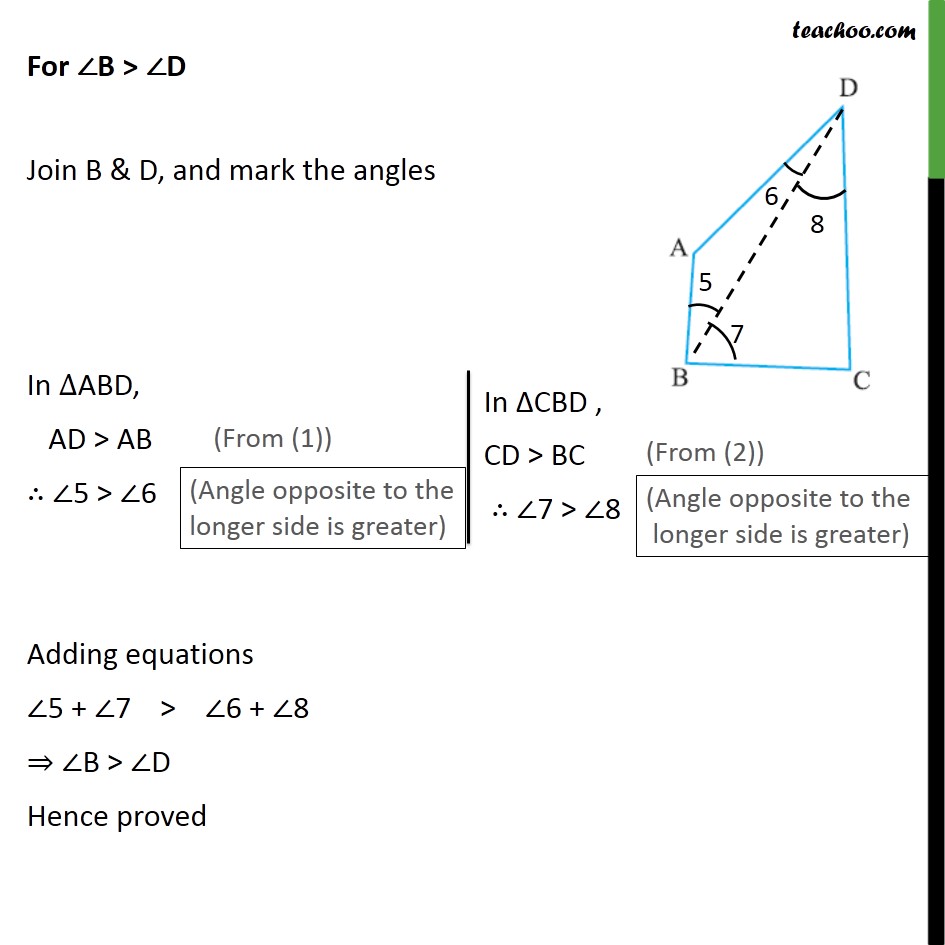
Question 4 - Side inequality - Chapter 7 Class 9 Triangles

Last updated at April 16, 2024 by

Ex 7.4, 4 - AB and CD are respectively smallest and longest - Ex 7.4

Ex 7.4, 4 - Chapter 7 Class 9 Triangles - Part 2
Ex 7.4, 4 - Chapter 7 Class 9 Triangles - Part 3

Transcript

Ex7.4, 4 AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D. Given: AB is the smallest side CD is the longest side To prove: ∠A > ∠C & ∠B > ∠D Proof: Join A & C, and mark the angles In ∆ABC, BC > AB ∴ ∠1 > ∠2 Adding equations ∠1 + ∠3 > ∠2 + ∠4 ∠A > ∠C Now, solving for ∠ B > ∠ D For ∠B > ∠D Join B & D, and mark the angles In ∆ABD, AD > AB ∴ ∠5 > ∠6 Adding equations ∠5 + ∠7 > ∠6 + ∠8 ⇒ ∠B > ∠D Hence proved

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.