You are here
Ex 7.3, 5 - Chapter 7 Class 9 Triangles
Last updated at Dec. 13, 2024 by Teachoo
Transcript
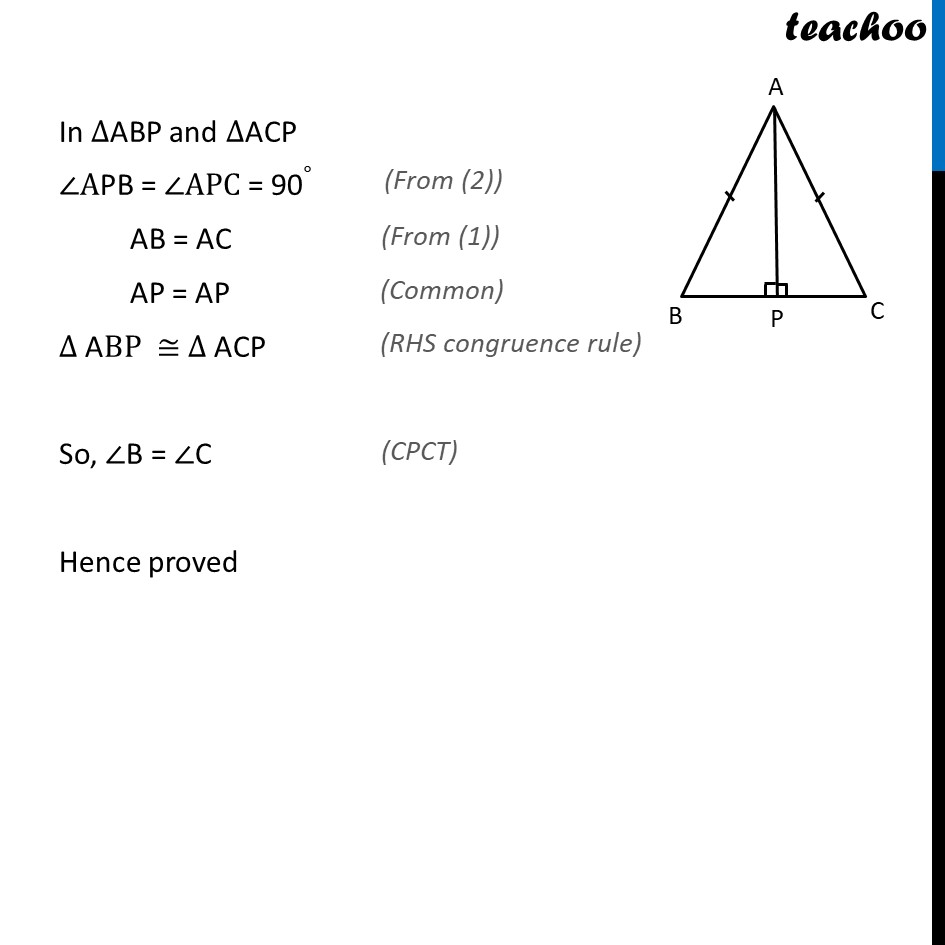
Ex 7.3,5 ABC is an isosceles triangle with AB = AC . Draw AP ⊥ BC to show that ∠𝐵 = ∠𝐶. Given: Since ∆ ABC is isosceles AB = AC Given AP ⊥ BC , So, ∠APB = ∠APC = 90∘ To prove: ∠ B = ∠ C Proof: In ∆ABP and ∆ACP ∠APB = ∠APC = 90∘ AB = AC AP = AP ∆ ABP ≅ ∆ ACP So, ∠B = ∠C Hence proved
