
Last updated at December 13, 2024 by Teachoo


Transcript
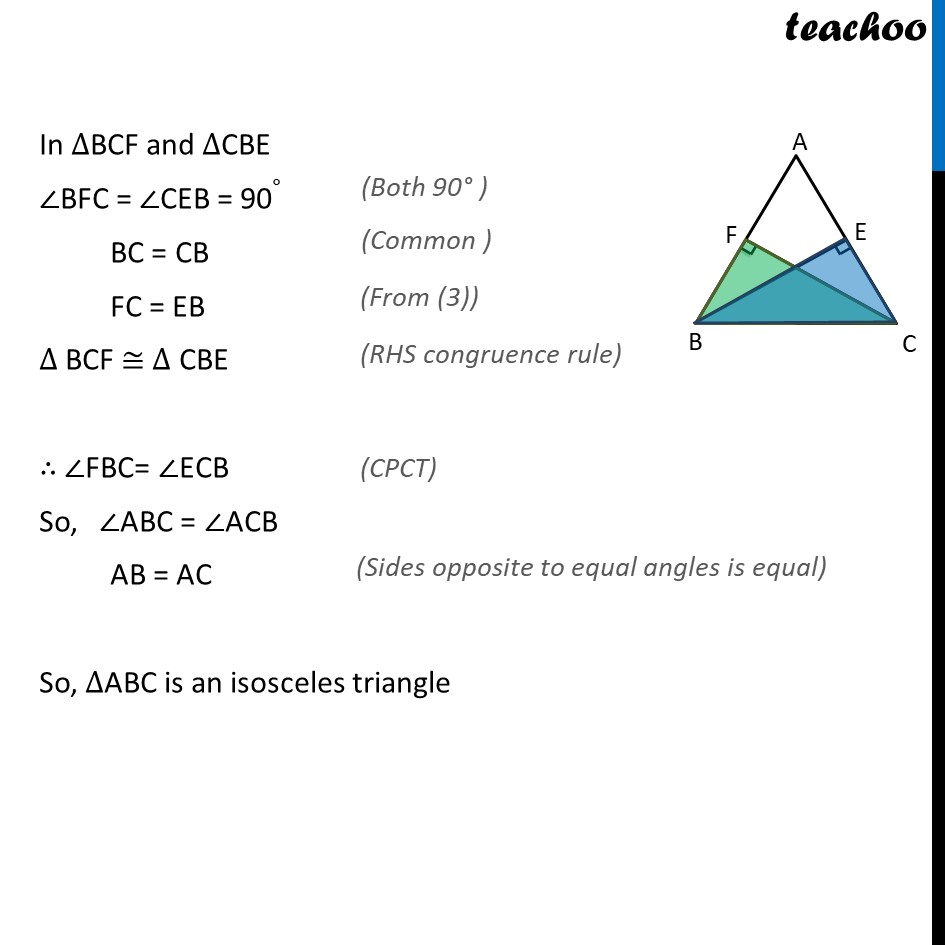
Ex 7.3,4 BE and CF are two equal altitudes of a triangle ABC . Using RHS congruence rule , prove that the triangle ABC is isosceles . Given: Given BE is a altitude, So, ∠𝐴EB = ∠CEB= 90∘ Also, CF is a altitude, So, ∠𝐴FC = ∠BFC= 90∘ Also, BE = CF To prove: Δ ABC is isoceles Proof: In ∆BCF and ∆CBE ∠BFC = ∠CEB = 90∘ BC = CB FC = EB ∆ BCF ≅ ∆ CBE ∴ ∠FBC= ∠ECB So, ∠ABC = ∠ACB AB = AC So, ∆ABC is an isosceles triangle