You are here
Ex 7.2, 4 - Chapter 7 Class 9 Triangles
Last updated at August 14, 2026 by Teachoo
Opposite Angles of equal sides
Chapter 7 Class 9 Triangles
Concept wise
- Congruency - Introduction
- SAS
- ASA/AAS
-
Opposite Angles of equal sides
- SSS
- RHS
- Side inequality
Transcript
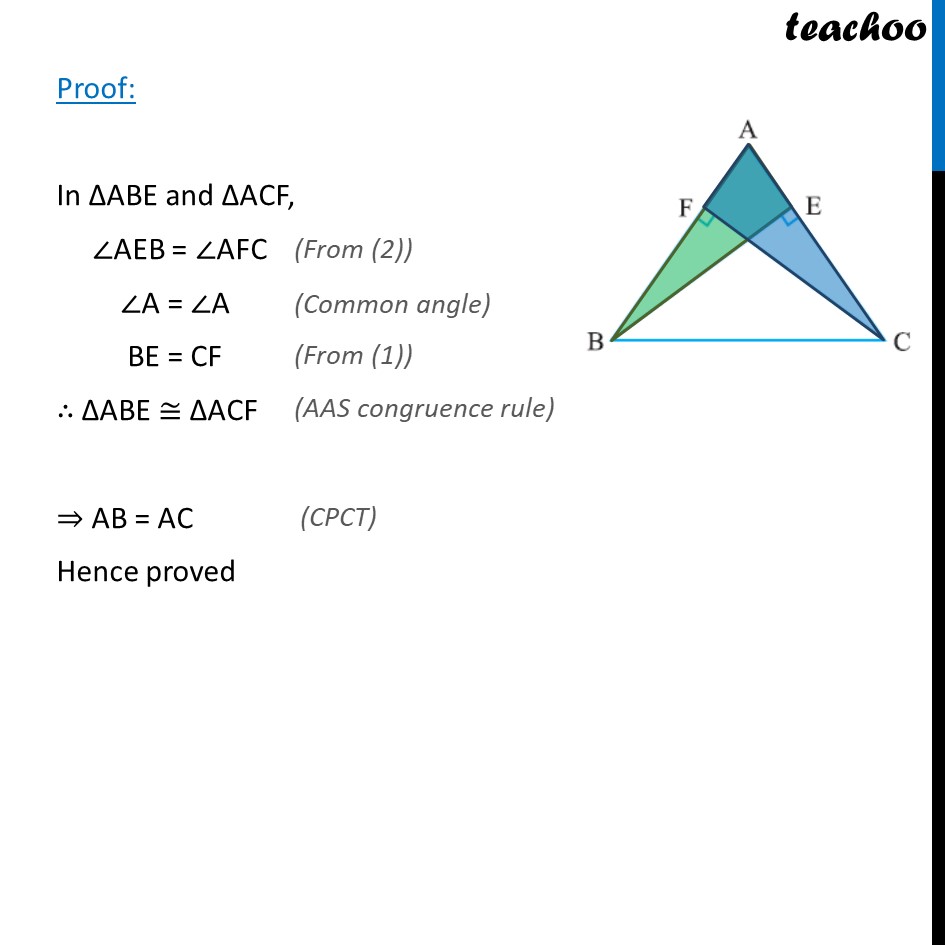
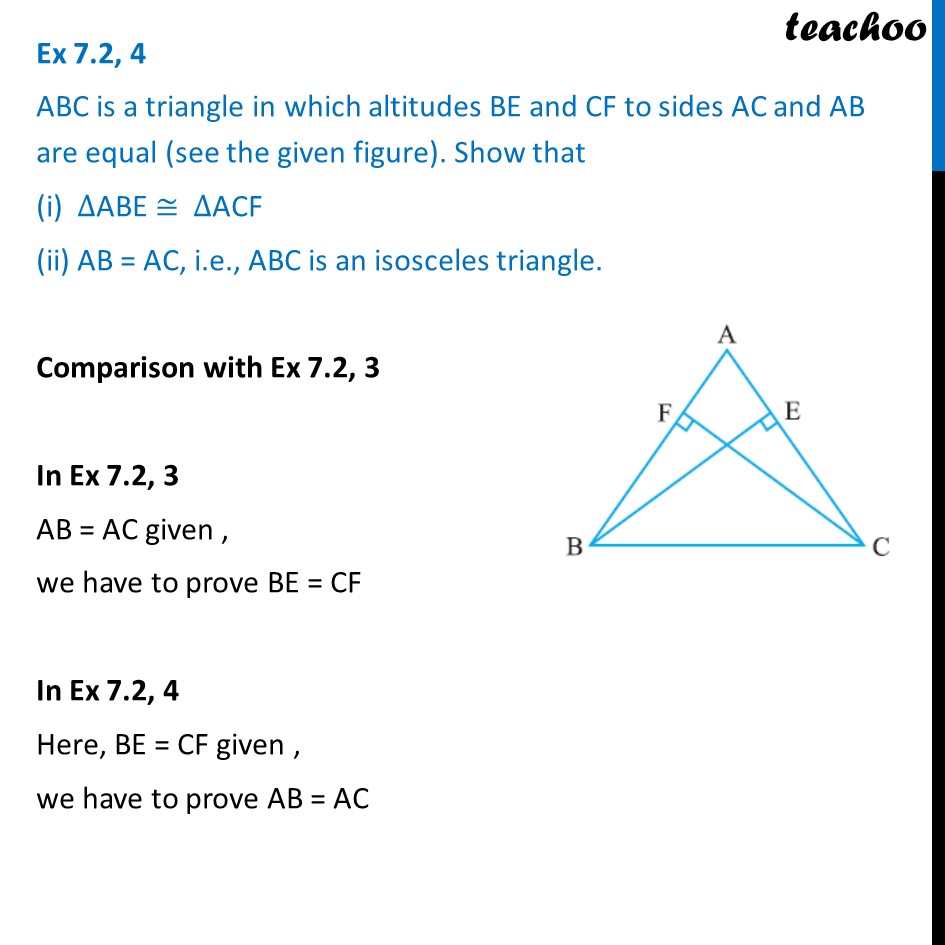
Ex7.2, 4 ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that (i) ABE ACF (ii) AB = AC, i.e., ABC is an isosceles triangle. Comparison with Ex 7.2 , 3 In Ex 7.2 , 3 AB = AC given , we have to prove BE = CF In Ex 7.2 , 4 Here, BE = CF given , we have to prove AB = AC Ex7.2, 4 ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that (i) ABE ACF (ii) AB = AC, i.e., ABC is an isosceles triangle. Given: BE = CF BE and CF are altitudes. So, AEB = 90 and AFC = 90 To prove: ABE ACF & AB = AC Proof: In ABE and ACF, AEB = AFC A = A BE = CF ABE ACF AB = AC Hence proved
