Ex 7.1, 5 - Chapter 7 Class 9 Triangles (Important Question)

Last updated at July 31, 2026 by

Ex 7.1, 5 - Line l is bisector of angle A and B is any point - Ex 7.1

part 2 - Ex 7.1, 5 - Ex 7.1 - Serial order wise - Chapter 7 Class 9 Triangles

Remove Ads

Transcript

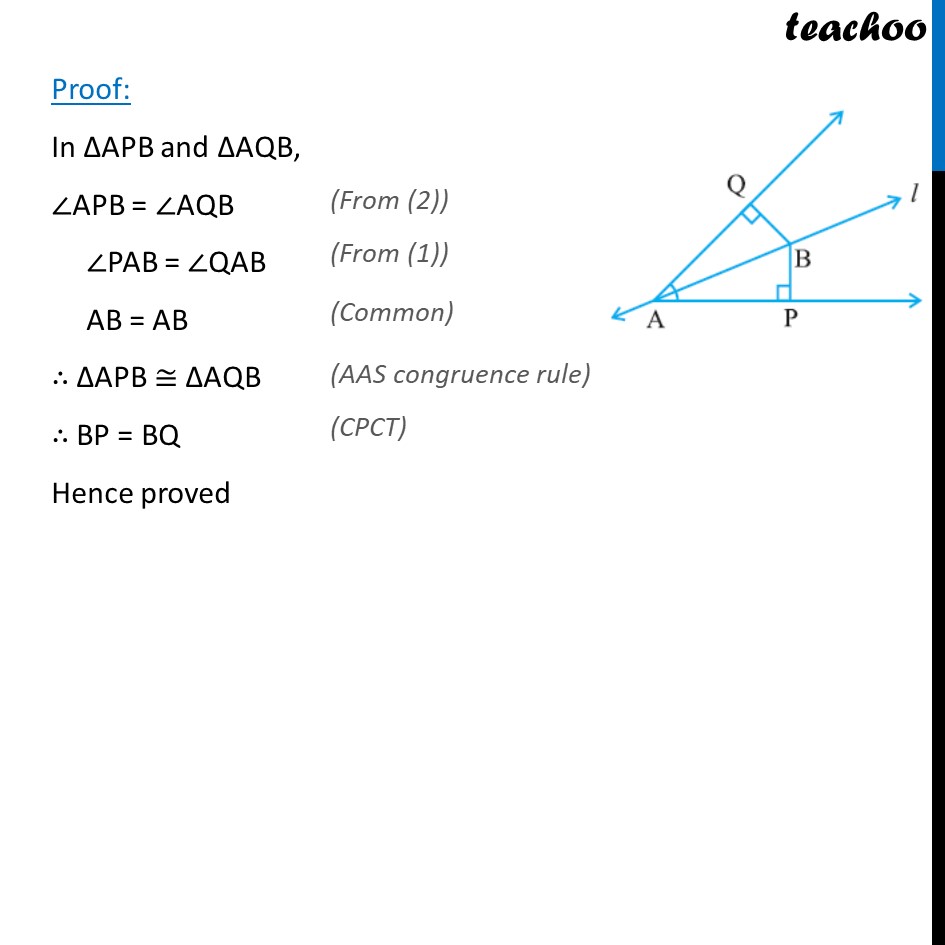
Ex7.1, 5 Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of A (see the given figure). Show that: (i) APB AQB (ii) BP = BQ or B is equidistant from the arms of A. Given: l is the bisector of A So, PAB = QAB BP & BQ are perpendiculars from B, So, APB = AQB = 90 To prove: (i) APB AQB (ii) BP = BQ Proof: In APB and AQB, APB = AQB PAB = QAB AB = AB APB AQB BP = BQ Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.

Many students prefer Teachoo Black for a smooth, ad-free learning experience.