Question 2 - Triangle - Problems - Chapter 6 Class 9 Lines and Angles

Transcript

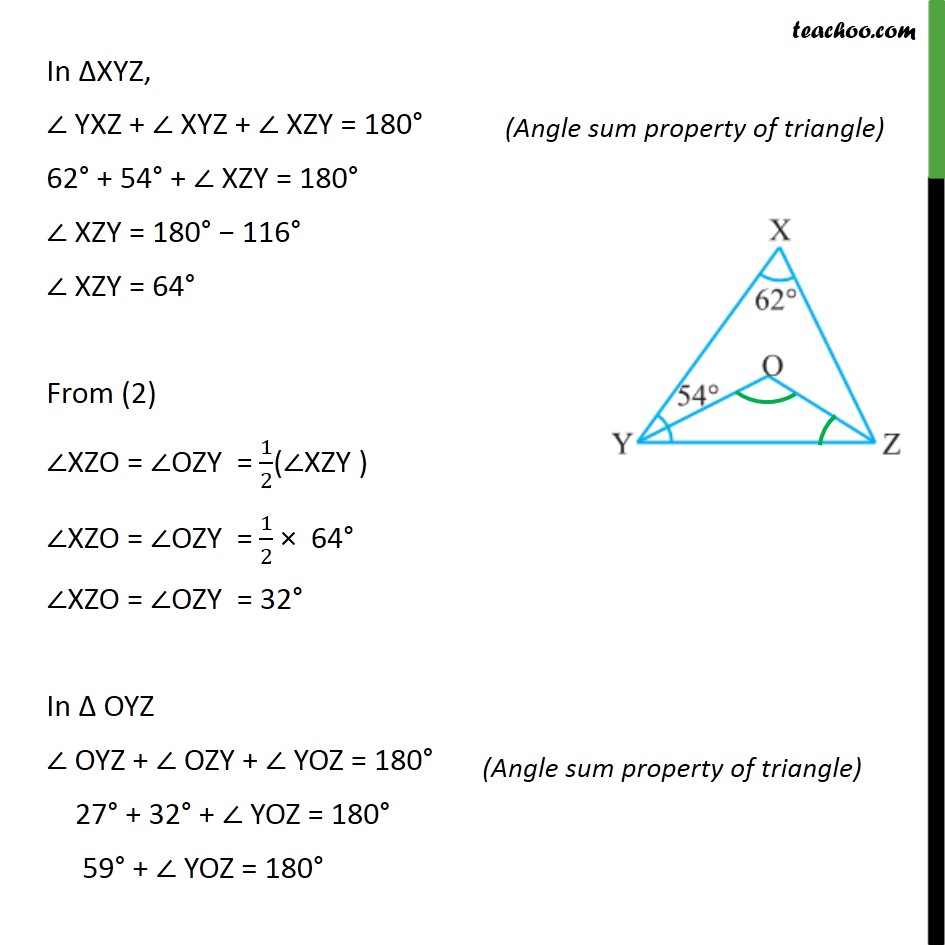
Question 2 In the given figure, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ. Given, OY is the angle bisector of ∠XYZ So, ∠XYO = ∠OYZ = 1/2(∠XYZ ) ∠XYO = ∠OYZ = 1/2 (54°) ∠XYO = ∠OYZ = 27° Also, OZ is the angle bisector of ∠XZY So, ∠XZO = ∠OZY = 1/2(∠XZY ) In ΔXYZ, ∠ YXZ + ∠ XYZ + ∠ XZY = 180° 62° + 54° + ∠ XZY = 180° ∠ XZY = 180° − 116° ∠ XZY = 64° From (2) ∠XZO = ∠OZY = 1/2(∠XZY ) ∠XZO = ∠OZY = 1/2 × 64° ∠XZO = ∠OZY = 32° In Δ OYZ ∠ OYZ + ∠ OZY + ∠ YOZ = 180° 27° + 32° + ∠ YOZ = 180° 59° + ∠ YOZ = 180° 59° + ∠ YOZ = 180° ∠YOZ = 180° − 59° ∠YOZ = 121°