Ex 6.1, 5 - Chapter 6 Class 9 Lines and Angles

Transcript

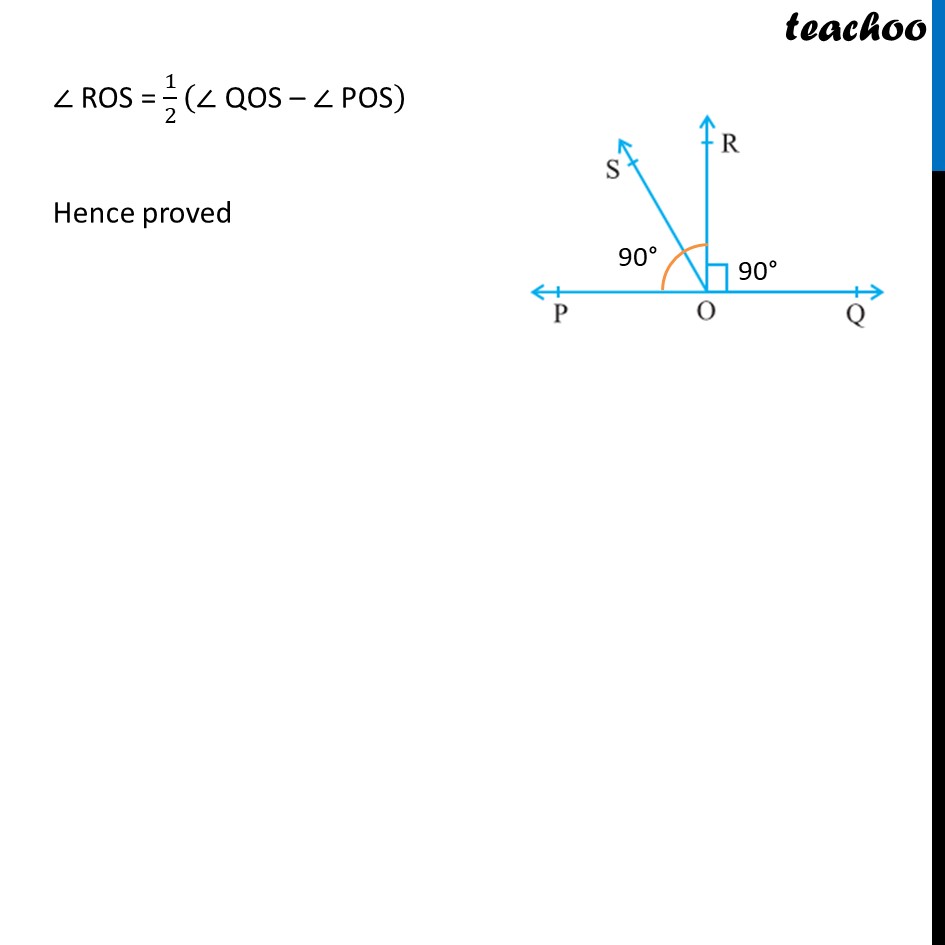
Ex 6.1, 5 In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2 (∠QOS – ∠POS ) Since OR ⊥ PQ Hence, ∠ ROP = 90° & ∠ ROQ = 90° We can say that ∠ ROP = ∠ ROQ ∠ POS + ∠ ROS = ∠ ROQ ∠ POS + ∠ ROS = ∠ QOS – ∠ ROS ∠ SOR + ∠ ROS = ∠ QOS – ∠ POS 2(∠ ROS) = ∠ QOS – ∠ POS ∠ ROS = 1/2 ("∠ QOS – ∠ POS" ) ∠ ROS = 1/2 ("∠ QOS – ∠ POS" ) Hence proved