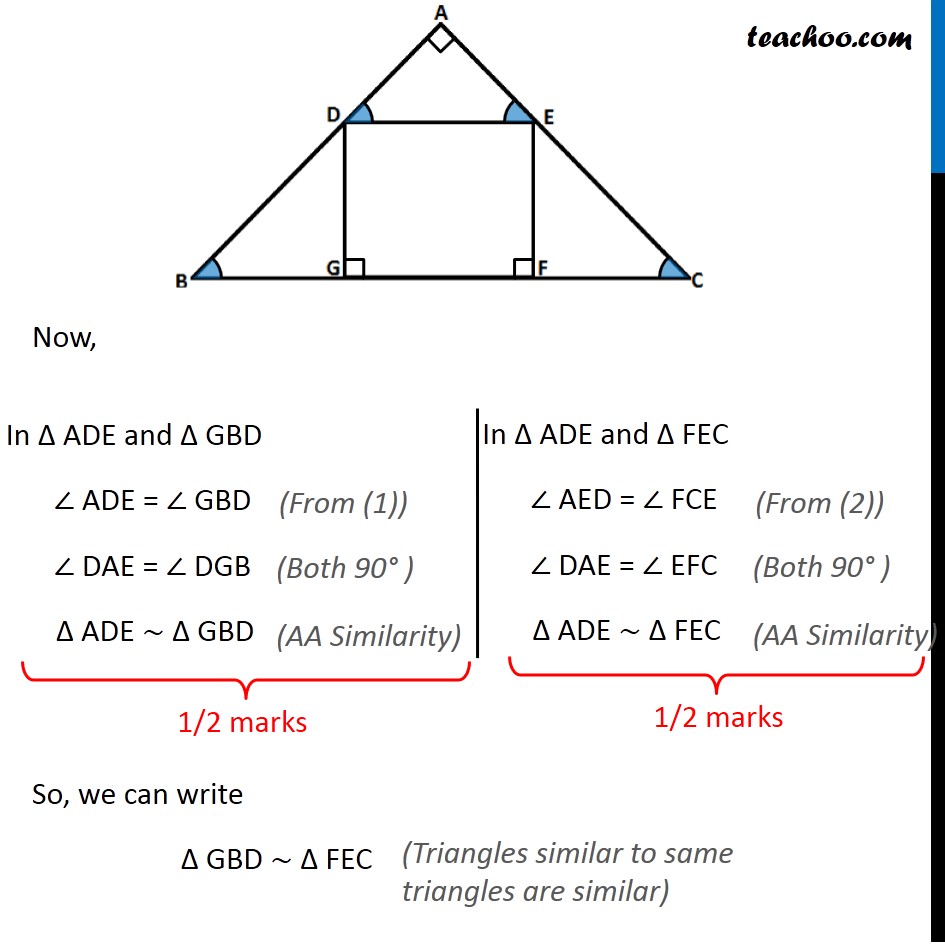
In the given figure, DEFG is a square and ∠BAC = 90°. Show that FG 2 = BG × FC


CBSE Class 10 Sample Paper for 2020 Boards - Maths Standard
CBSE Class 10 Sample Paper for 2020 Boards - Maths Standard
Last updated at February 27, 2025 by Teachoo




Transcript
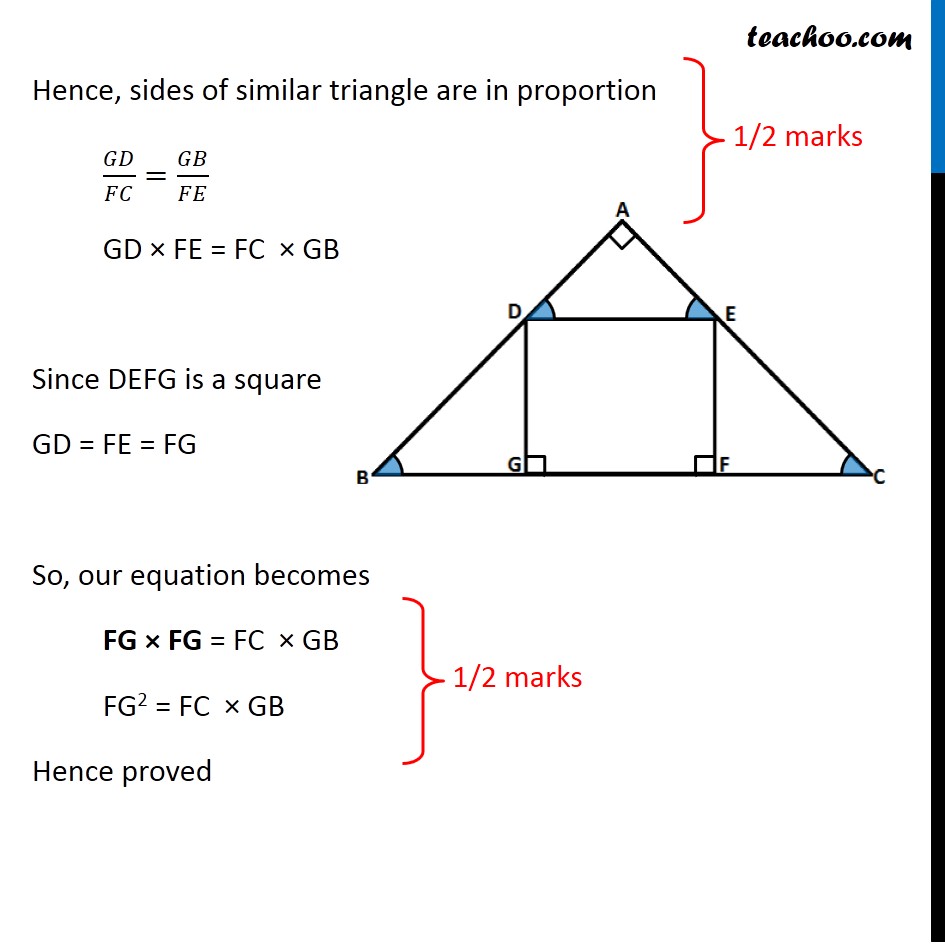
Question 23 (OR 1st question) In the given figure, DEFG is a square and ∠BAC = 90° . Show that FG2 = BG × FC Now, DE ∥ GF, So, we can say DE ∥ BC For parallel lines DE and BC, transversal AB ∠ ADE = ∠ GBD For parallel lines DE and BC, transversal AC ∠ AED = ∠ FCE Now, In Δ ADE and Δ GBD ∠ ADE = ∠ GBD ∠ DAE = ∠ DGB Δ ADE ∼ Δ GBD In Δ ADE and Δ FEC ∠ AED = ∠ FCE ∠ DAE = ∠ EFC Δ ADE ∼ Δ FEC So, we can write Δ GBD ∼ Δ FEC Hence, sides of similar triangle are in proportion 𝐺𝐷/𝐹𝐶=𝐺𝐵/𝐹𝐸 GD × FE = FC × GB Since DEFG is a square GD = FE = FG So, our equation becomes FG × FG = FC × GB FG2 = FC × GB Hence proved