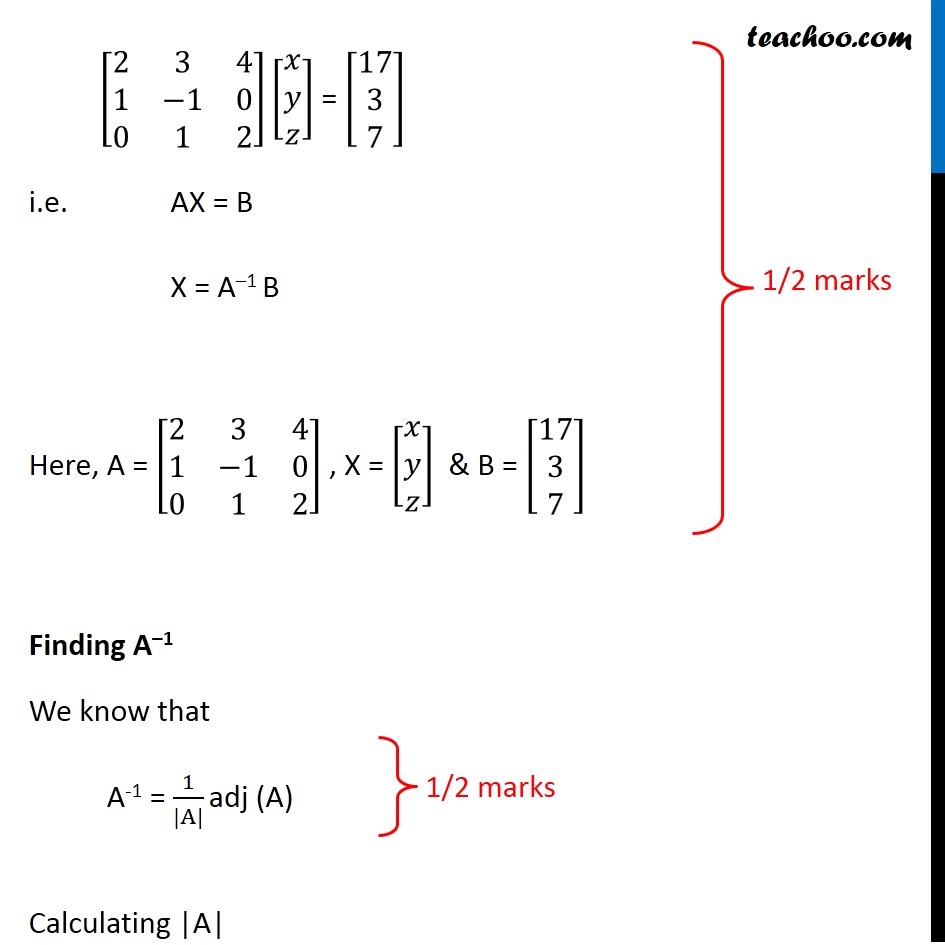
If A = |2 3 4 1 -1 0 0 1 2|, find A − 1 . Hence, solve the system of equations
x − y = 3
2x + 3y + 4z = 17
y + 2z = 7



CBSE Class 12 Sample Paper for 2020 Boards
CBSE Class 12 Sample Paper for 2020 Boards
Last updated at Dec. 16, 2024 by Teachoo






Transcript
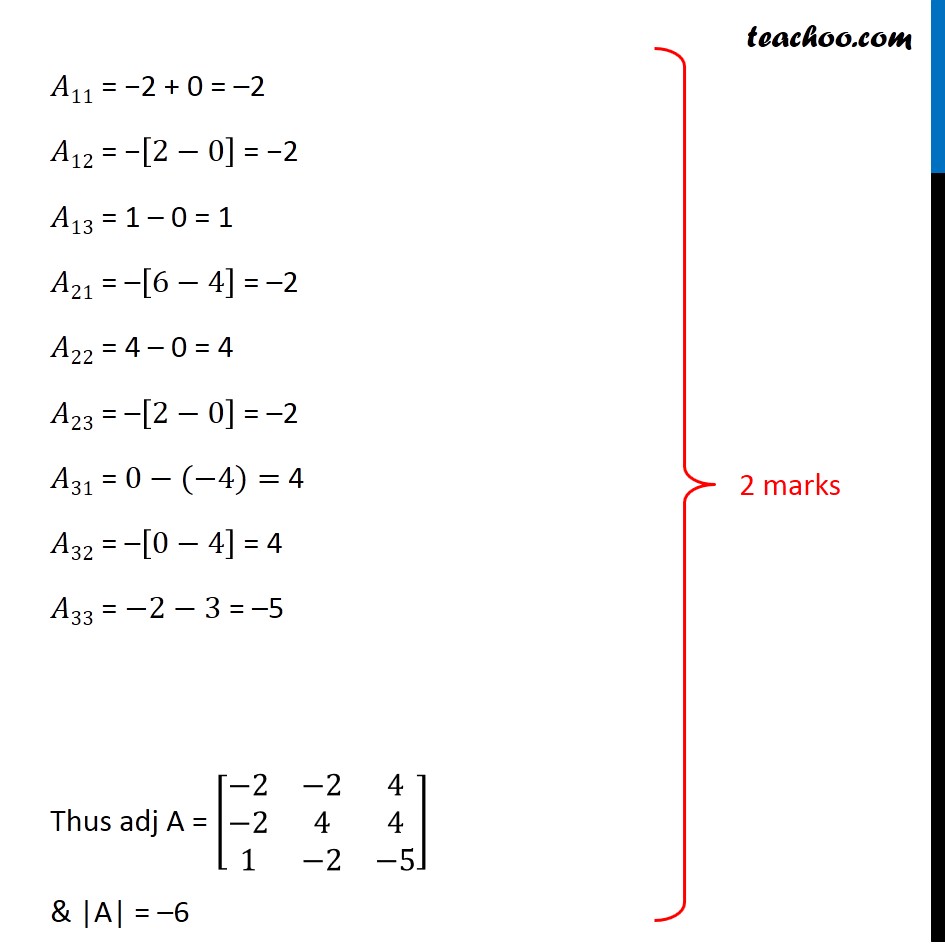
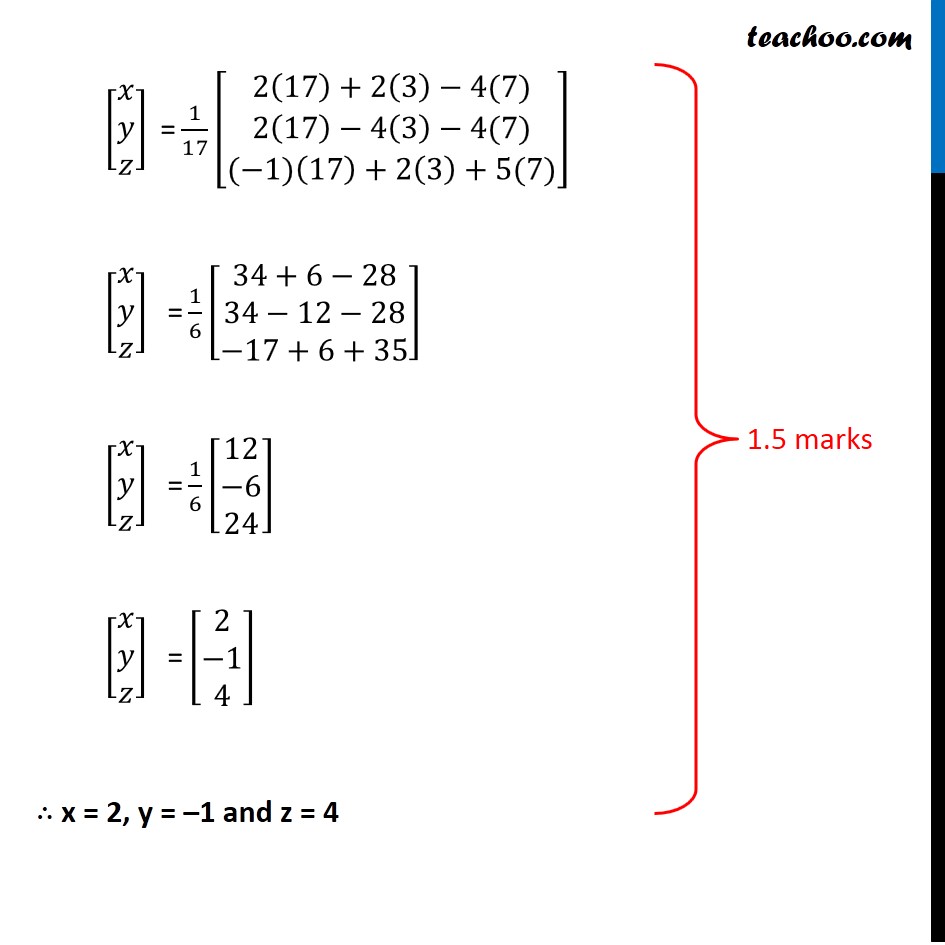
Question 33 (OR 2nd Question) If A = |2 3 4 1 -1 0 0 1 2|, find A− 1. Hence, solve the system of equations x − y = 3 2x + 3y + 4z = 17 y + 2z = 7 The equations can be written as 2x + 3y + 4z = 17 x − y = 3 y + 2z = 7 So, the equation is in the form of [2 3 4 1 -1 0 0 1 2] [ x y z] [17 3 7] i.e. AX = B X = A–1 B Here, A = [ 2 3 4 1 -1 0 0 1 2], x = [x y z] & B = [17 3 7] Finding A–1 We know that A-1 = 1/(|A|) adj (A) Calculating |A| |A|= [ 2 3 4 1 -1 0 0 1 2] = 2(−2 – 0) − 3 (2 – 0) + 4 (1 – 0) = –4 – 6 + 4 = −6 Since |A|≠ 0 ∴ The system of equation is consistent & has a unique solution Now finding adj (A) adj A = [ A11 A12 A13 A21 A22 A23 A21 A22 A23 A31 A32 A33] [ A11 A21 A31 A12 A22 A32 A13 A23 A33 ] A = [ 2 3 4 1 -1 0 0 1 2] 𝐴11 = –2 𝐴12 = −2 𝐴13 = 1 𝐴21 = –2 𝐴22 = 4 𝐴23 = –2 𝐴31 = 4 𝐴32 = 4 𝐴33 = –5 𝐴11 = −2 + 0 = –2 𝐴12 = −[2−0] = −2 𝐴13 = 1 – 0 = 1 𝐴21 = –[6−4] = –2 𝐴22 = 4 – 0 = 4 𝐴23 = –[2−0] = –2 𝐴31 = 0−(−4)= 4 𝐴32 = –[0−4] = 4 𝐴33 = −2−3 = –5 Thus adj A = [ -2 -2 4 -2 4 4 1 -2 -5 & |A| = –6 Now, A-1 = 1/(|A|) adj A A-1 = 1/-6 [-2 -2 4 -2 4 4 1 -2 -5] = 1/6 [2 2 -4 2 -4 -4 -1 2 5] Now, X = A–1B [X Y Z] = 1/6 [ 2 2 -4 2 -4 -4 -1 2 5] [ 17 3 7] [ XY Z] = 1/6 [2 (17) + 2(3) - 4(7) 2 (17) - 4 (3) - 4(7) (-1) (17) + 2(3) + 5 (7) [X Y Z] = 1/17 [2 (17) + 2 (3) - 4 (7) 2(17) - 4 (3) - 4(7) (-1) (17) + 2(3) + 5(7) [X Y Z] = 1/6 [34 + 6 - 28 34 - 12 - 28 -17 + 6 + 35] [X Y Z] = 1/6 [ 12 -6 24] [X Y Z] = [2 -1 4] ∴ x = 2, y = –1 and z = 4