Question 27 - CBSE Class 12 Sample Paper for 2020 Boards

Transcript

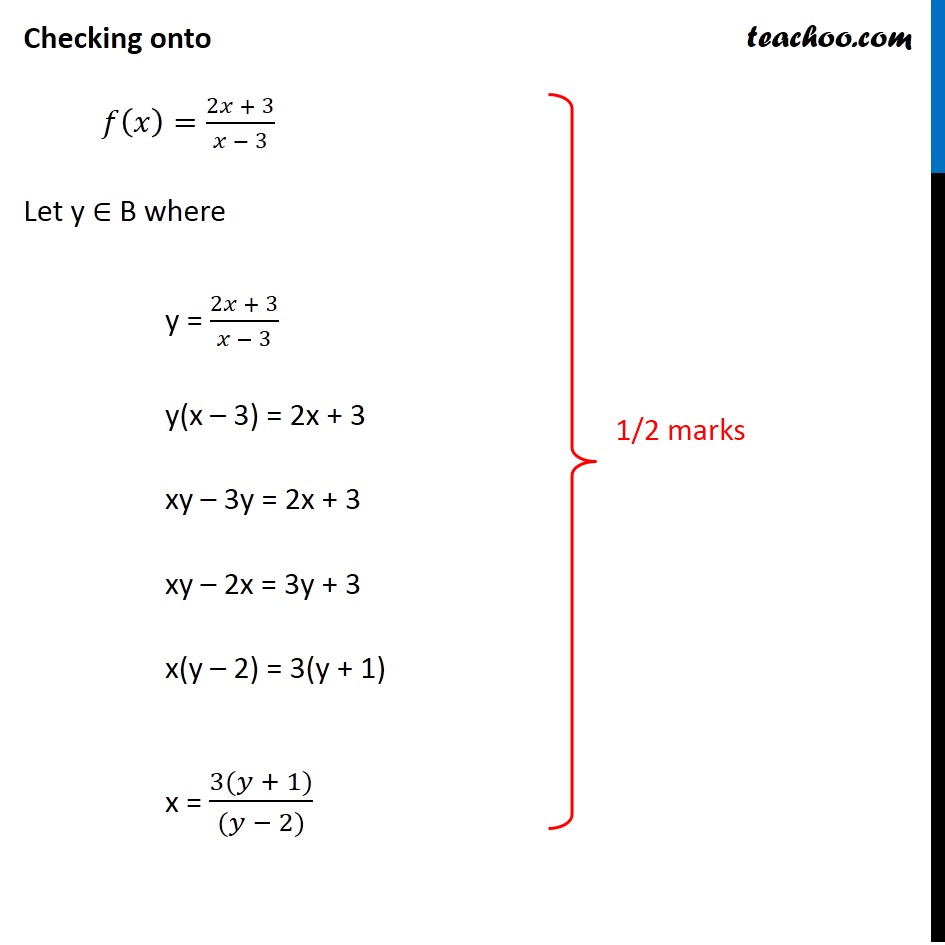
Question 27 Let 𝑓: A → B be a function defined as 𝑓(𝑥)=(2𝑥 + 3)/(𝑥 − 3) , where A = R − {3} and B = R − {2}. Is the function f one–one and onto? Is f invertible? If yes, then find its inverse 𝑓(𝑥)=(2𝑥 + 3)/(𝑥 − 3) Checking one-one Let 𝑥_1 , 𝑥_2 ∈ A 𝑓(𝑥_1 )=(2𝑥_1+ 3)/(𝑥_1− 3) 𝑓(𝑥_2 )=(2𝑥_2+ 3)/(𝑥_2 − 3) One-one Steps 1. Calculate f(x1) 2. Calculate f(x2) 3. Putting f(x1) = f(x2) we have to prove x1 = x2 Putting 𝑓(𝑥_1 ) = 𝑓(𝑥_2 ) (2𝑥_1+ 3)/(𝑥_1− 3) = (2𝑥_2+ 3)/(𝑥_2 − 3) (2𝑥_1+ 3) (𝑥_2 − 3) = (2𝑥_2+ 3) (𝑥_1 − 3) 2𝑥_1 "(" 𝑥_2 − 3")"+ 3 (𝑥_2 − 3) = 2𝑥_2 "(" 𝑥_1 − 3")"+ 3(𝑥_1 − 3) 2𝑥_1 𝑥_2 −6𝑥_1+ 3𝑥_2−9 = 2𝑥_2 𝑥_1 −6𝑥_2+ 3𝑥_1 −9 −6𝑥_1+ 3𝑥_2 = −6𝑥_2+ 3𝑥_1 3𝑥_2+6𝑥_2 = 3𝑥_1+6𝑥_1 9𝑥_2= 9𝑥_1 𝑥_2= 𝑥_1 If 𝑓(𝑥_1 ) = 𝑓(𝑥_2 ) , then 𝑥_1= 𝑥_2 ∴ f is one-one Checking onto 𝑓(𝑥)=(2𝑥 + 3)/(𝑥 − 3) Let y ∈ B where y = (2𝑥 + 3)/(𝑥 − 3) y(x – 3) = 2x + 3 xy – 3y = 2x + 3 xy – 2x = 3y + 3 x(y – 2) = 3(y + 1) x = (3(𝑦 + 1))/((𝑦 − 2)) For y = 2 , x is not defined But it is given that y ∈ R – {2} Hence , x = (3(𝑦 + 1))/((𝑦 − 2)) ∈ R – {3} Now, Checking for y = f(x) Putting value of x in f(x) f(x) = f((3(𝑦 + 1))/((𝑦 − 2))) = (2(3(𝑦 + 1)/((𝑦 − 2) ))+ 3)/((3(𝑦 + 1)/((𝑦 − 2) ))− 3) = (((6(𝑦 + 1)+3(𝑦−2))/((𝑦 − 2) )))/((3(𝑦 + 1)/((𝑦 − 2) ))− 3) Also, y = f(x) Putting y in f(x) Hence, f is onto = (2(3(𝑦 + 1)/((𝑦 − 2) ))+ 3)/((3(𝑦 + 1)/((𝑦 − 2) ))− 3) = (((6(𝑦 + 1) + 3(𝑦 − 2))/((𝑦 − 2) )))/(((3(𝑦 + 1) − 3(𝑦 − 2))/((𝑦 − 2) )) ) = (6(𝑦 + 1) + 3(𝑦 − 2))/(3(𝑦 + 1) − 3(𝑦 − 2)) = (6𝑦 + 6 + 3𝑦 − 6)/(3𝑦 + 3 − 3𝑦 + 6) = 9𝑦/9 = y Thus, for every y ∈ B, there exists x ∈ A such that f(x) = y Hence, f is onto Since f(x) is one-one and onto, So, f(x) is invertible And Inverse of x = 𝑓^(−1) (𝑦) = (3(𝑦 + 1))/((𝑦 − 2))