Question 4 Page 216 - Chapter 12 Class 10 - Electricity

Transcript

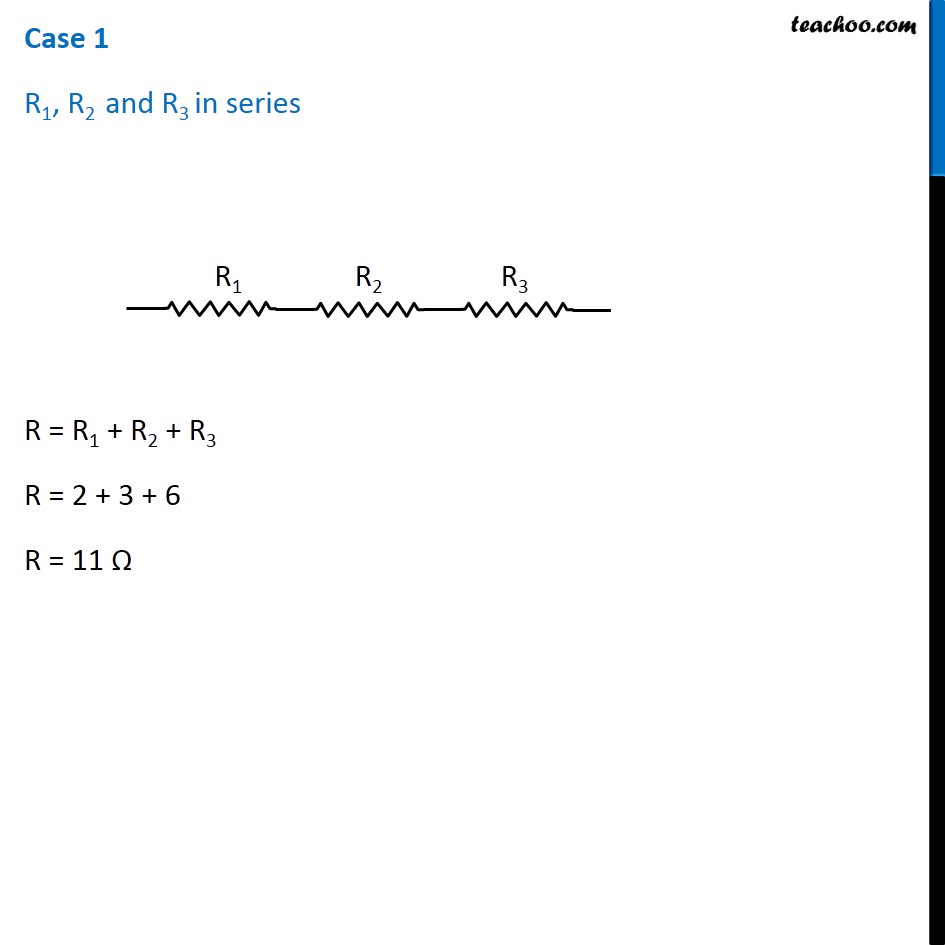
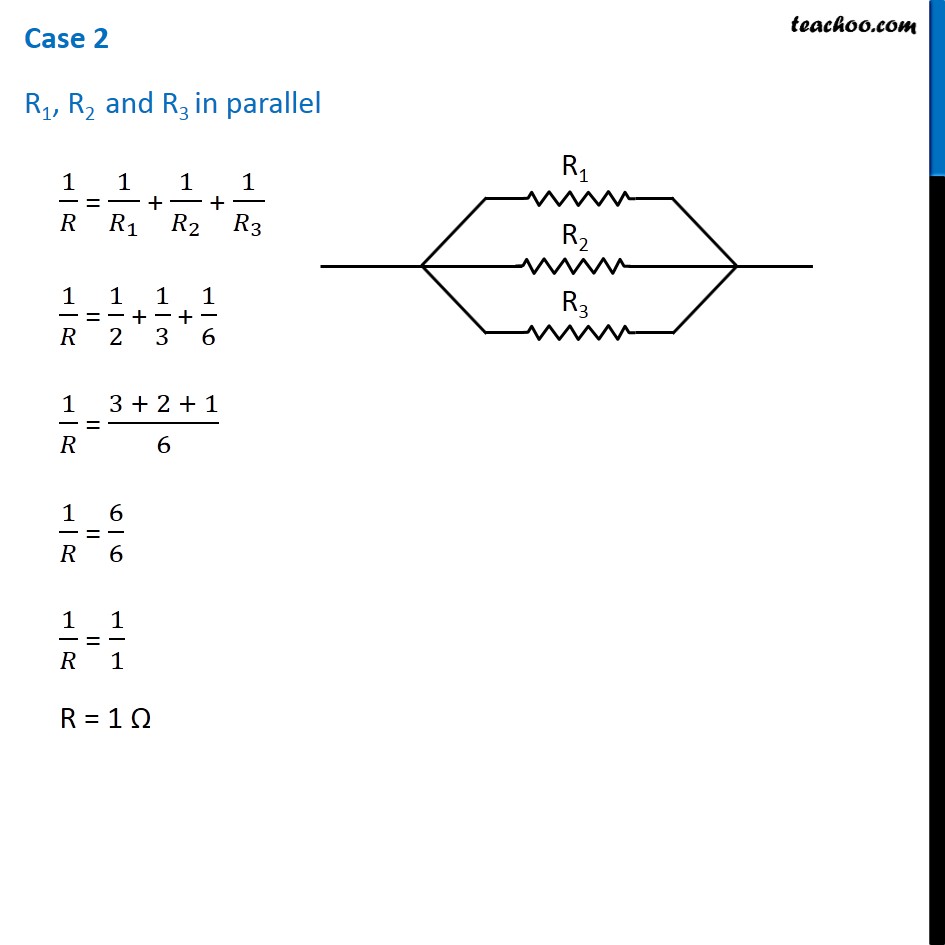
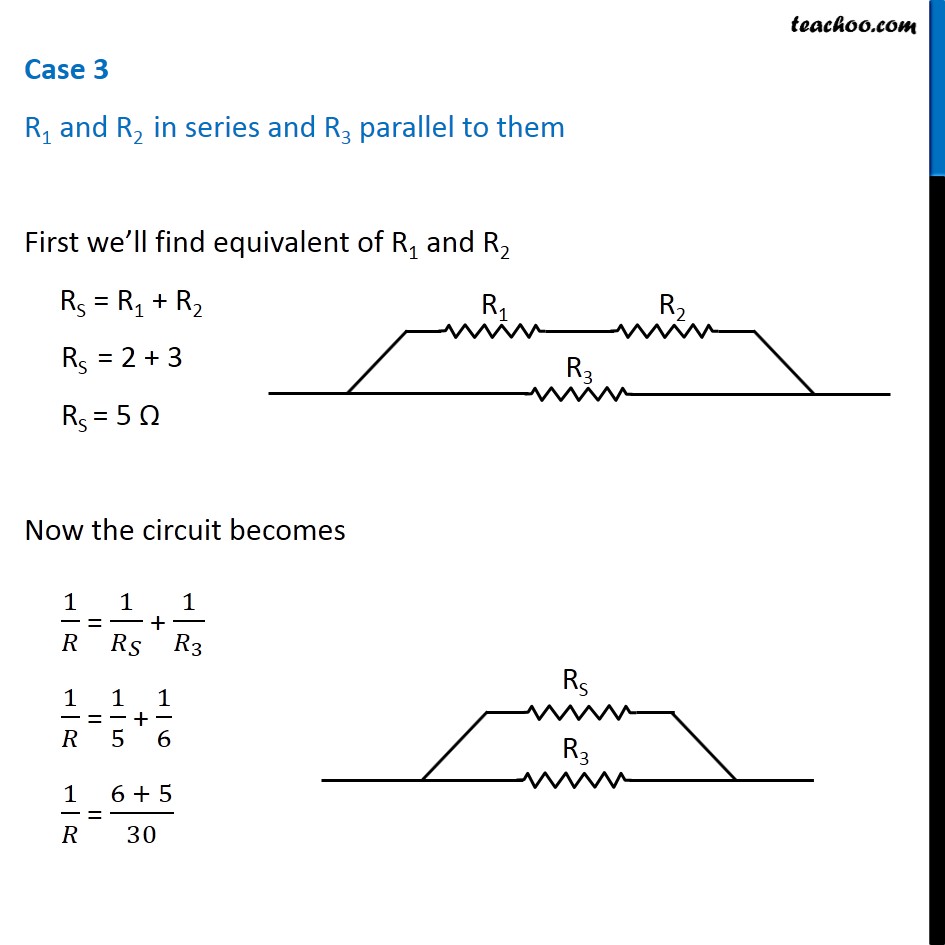
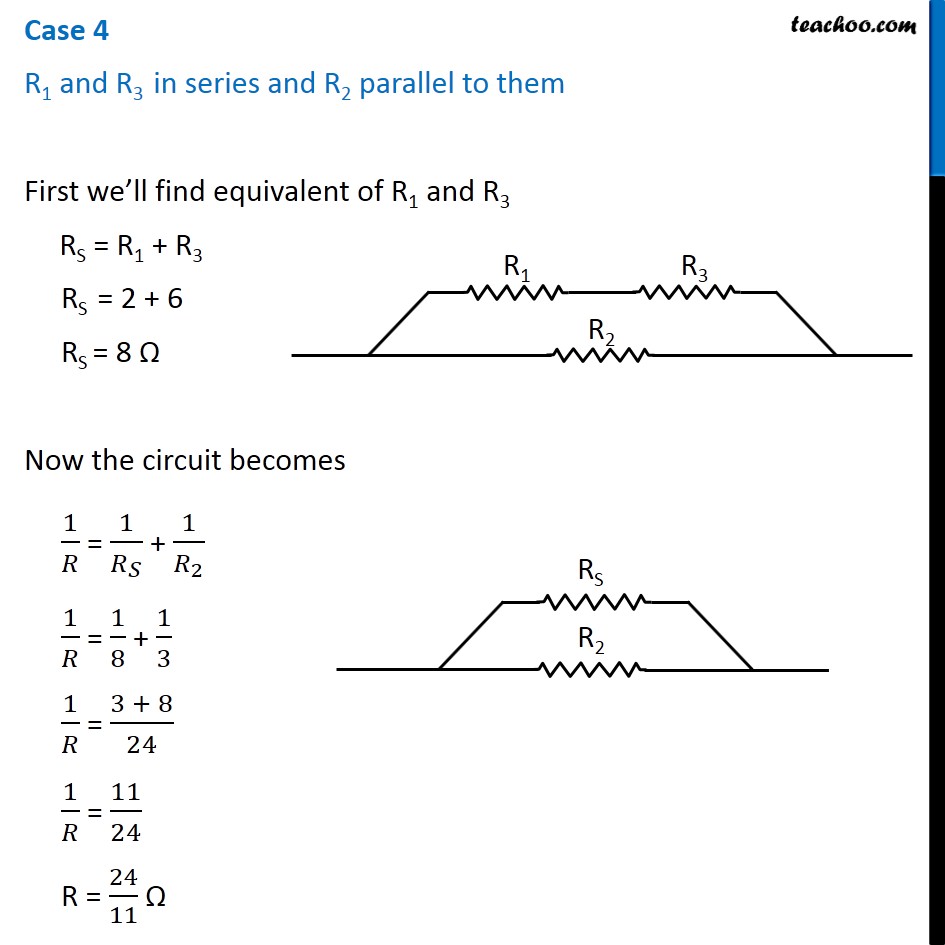
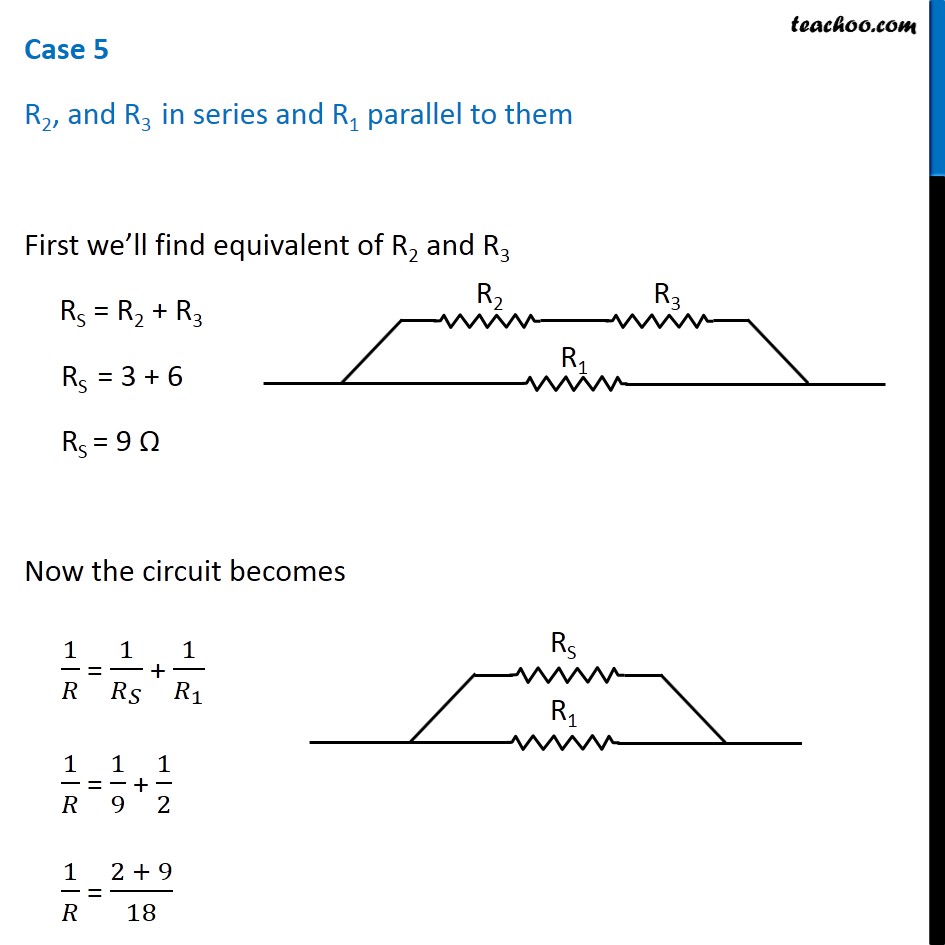
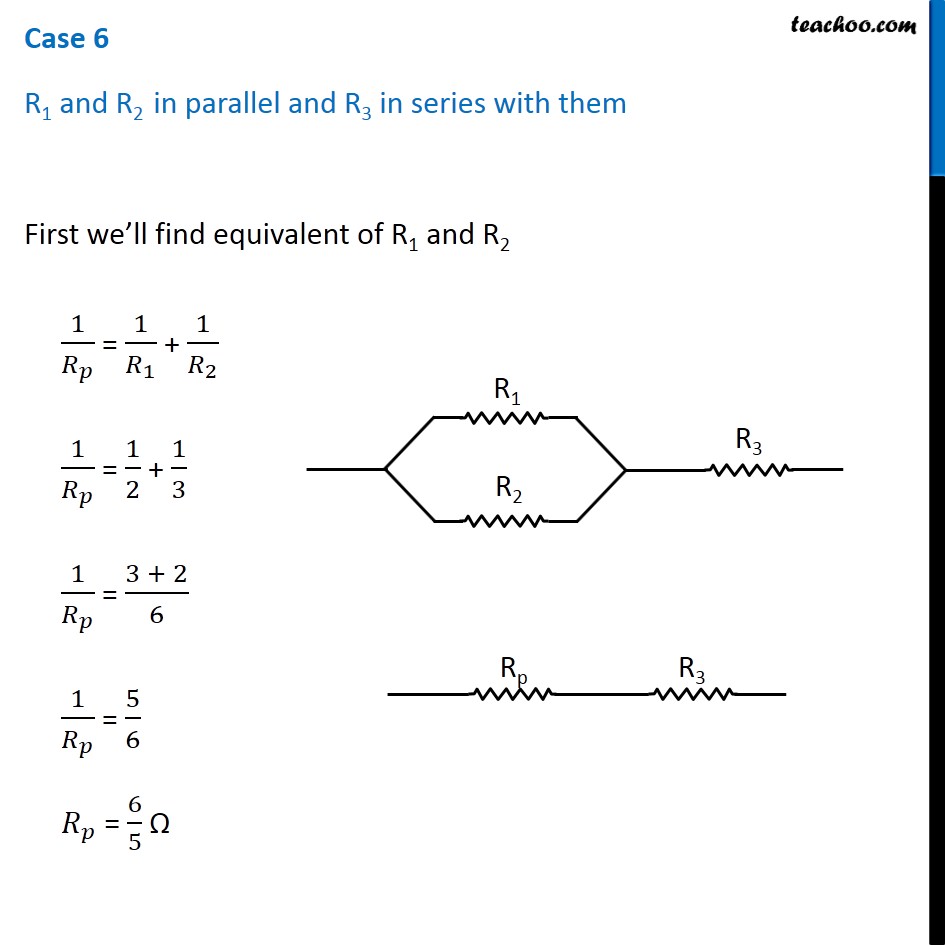
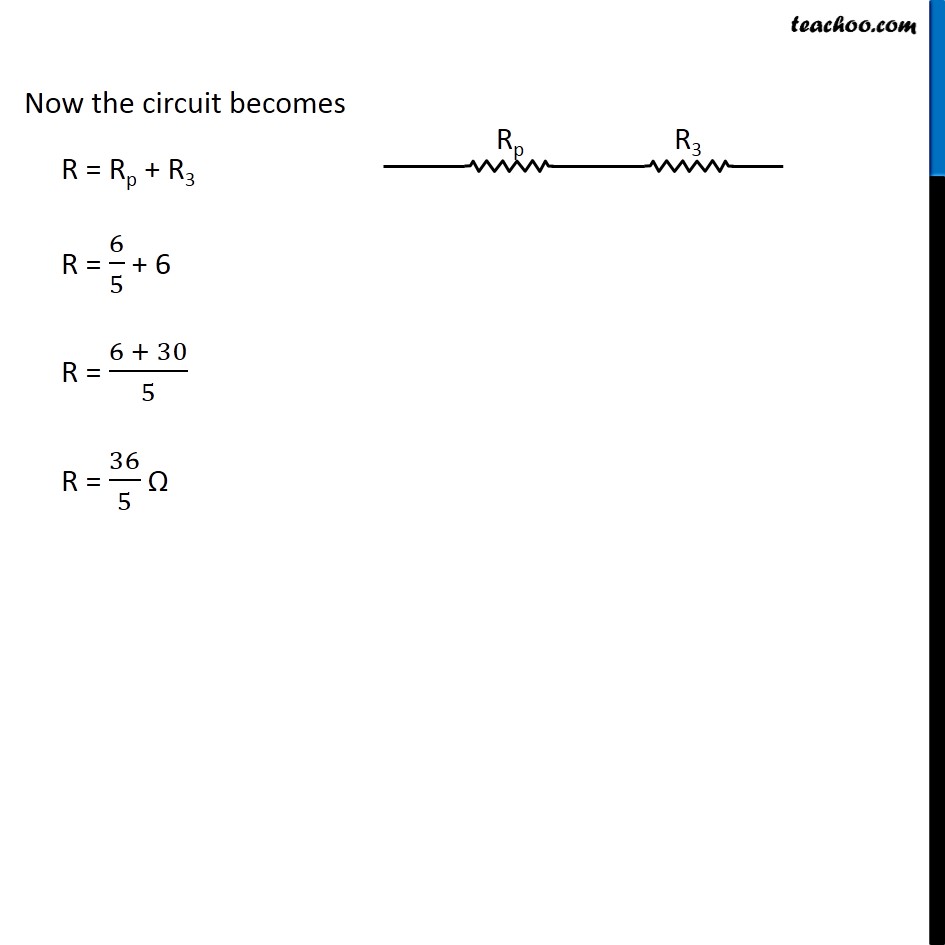
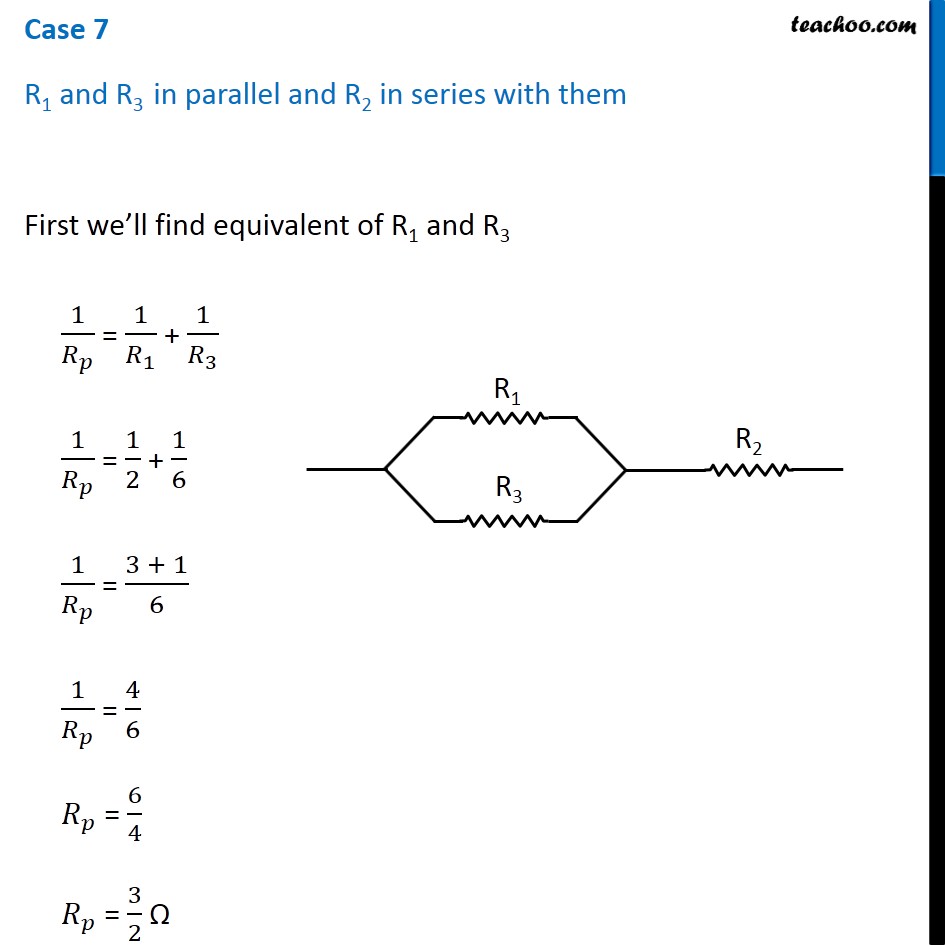
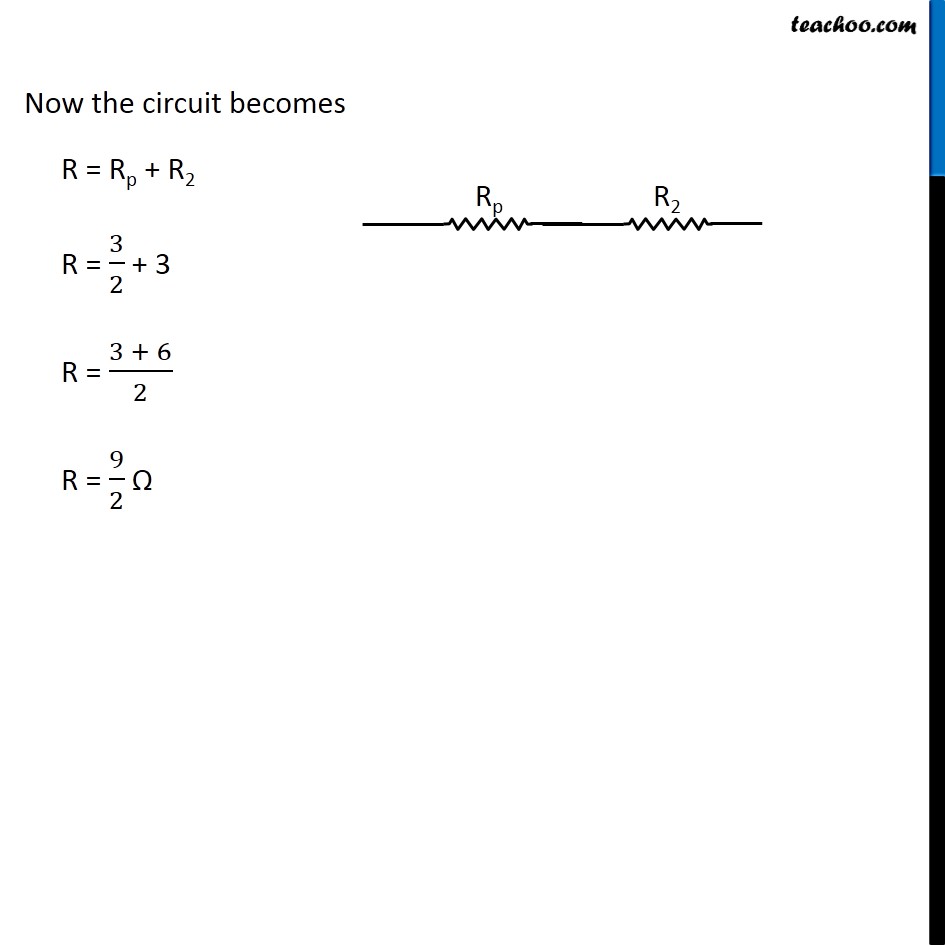
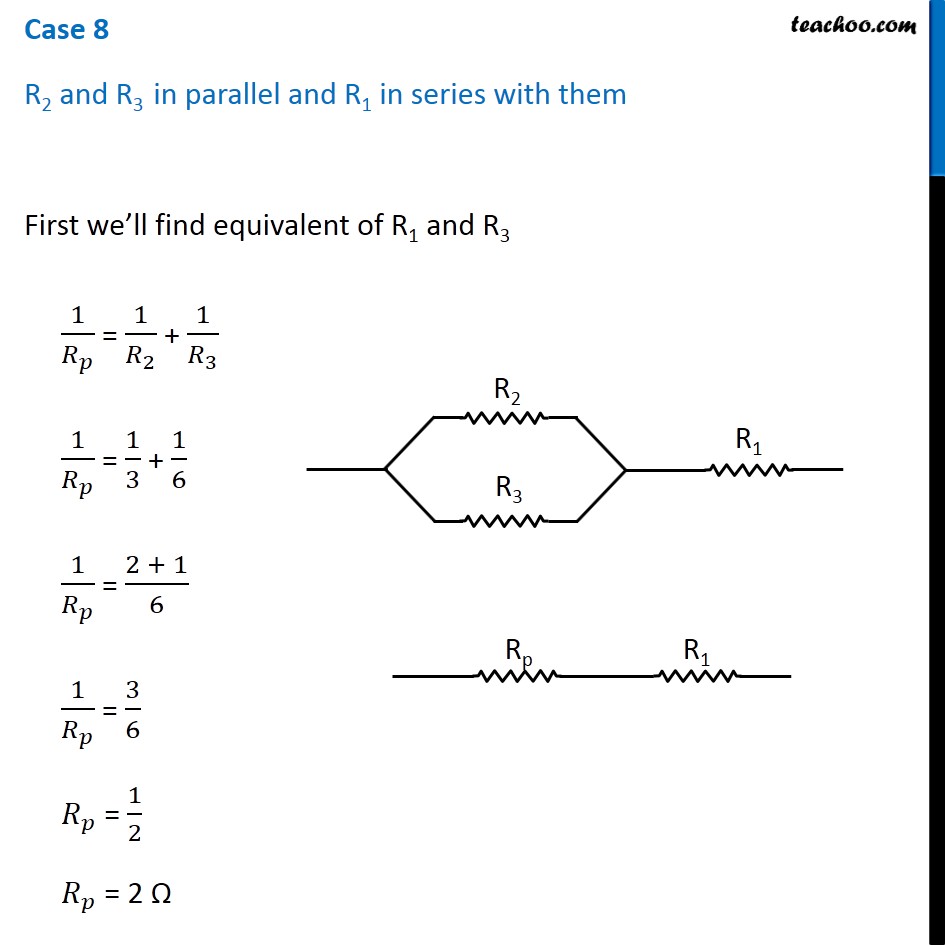
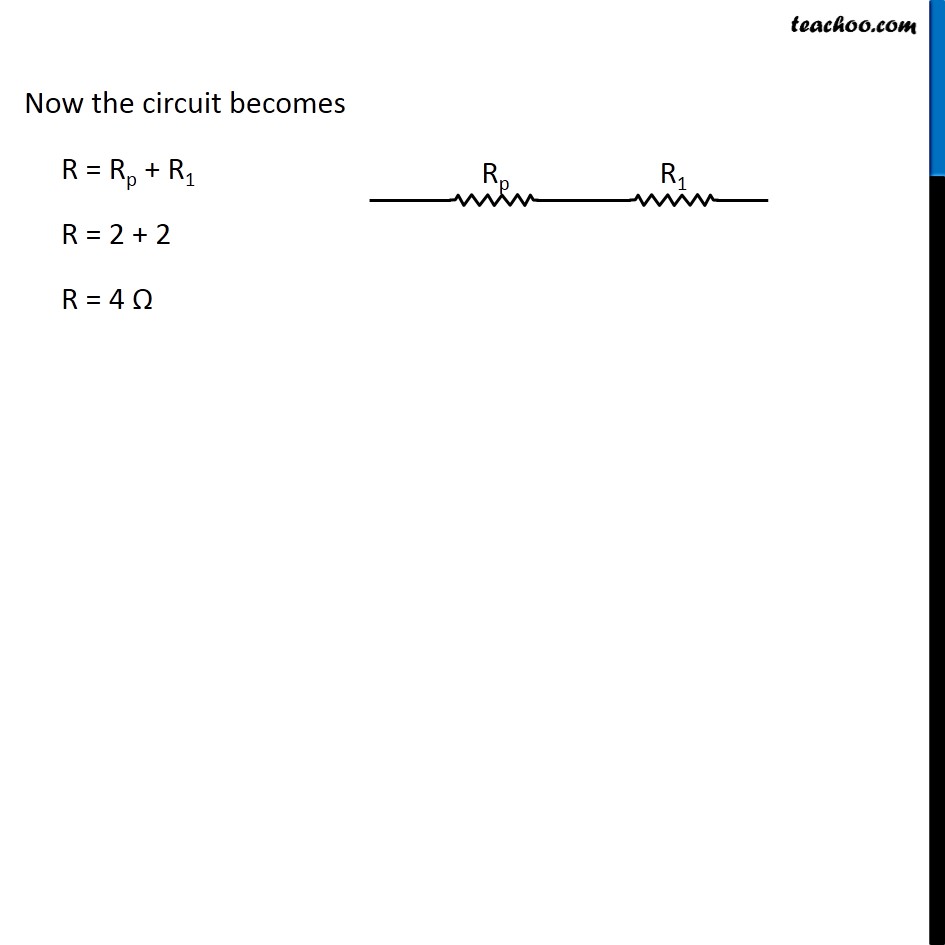
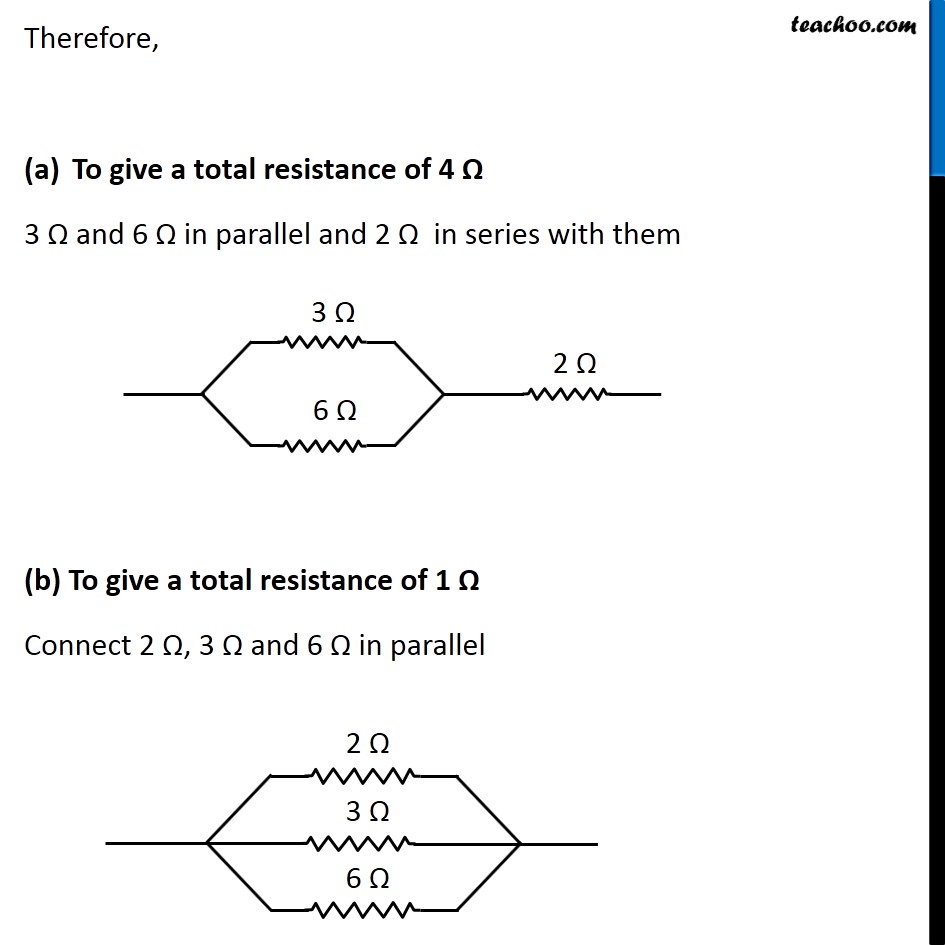
Question 4 Page 216 How can three resistors of resistances 2 Ω, 3 Ω, and 6 Ω be connected to give a total resistance of (a) 4 Ω, (b) 1 Ω? Let R1 = 2 Ω R2 = 3 Ω R3 = 6 Ω The three resistors can be arranged in 8 ways All 3 parallel All 3 in series 2 parallel, 1 series - 3 cases 2 series, 1 parallel - 3 cases In series combination, equivalent resistance is given by Rs = R1 + R2 + R3 In parallel combination, equivalent resistance is given by 1/𝑅_𝑃 = 1/𝑅_1 + 1/𝑅_2 + 1/𝑅_3 Case 1 R1, R2 and R3 in series R = R1 + R2 + R3 R = 2 + 3 + 6 R = 11 Ω Case 2 R1, R2 and R3 in parallel 1/𝑅 = 1/𝑅_1 + 1/𝑅_2 + 1/𝑅_3 1/𝑅 = 1/2 + 1/3 + 1/6 1/𝑅 = (3 + 2 + 1)/6 1/𝑅 = 6/6 1/𝑅 = 1/1 R = 1 Ω Case 3 R1 and R2 in series and R3 parallel to them First we’ll find equivalent of R1 and R2 RS = R1 + R2 RS = 2 + 3 RS = 5 Ω Now the circuit becomes 1/𝑅 = 1/𝑅_𝑆 + 1/𝑅_3 1/𝑅 = 1/5 + 1/6 1/𝑅 = (6 + 5)/30 1/𝑅 = 11/30 R = 30/11 Ω Case 4 R1 and R3 in series and R2 parallel to them First we’ll find equivalent of R1 and R3 RS = R1 + R3 RS = 2 + 6 RS = 8 Ω Now the circuit becomes 1/𝑅 = 1/𝑅_𝑆 + 1/𝑅_2 1/𝑅 = 1/8 + 1/3 1/𝑅 = (3 + 8)/24 1/𝑅 = 11/24 R = 24/11 Ω Case 5 R2, and R3 in series and R1 parallel to them First we’ll find equivalent of R2 and R3 RS = R2 + R3 RS = 3 + 6 RS = 9 Ω Now the circuit becomes 1/𝑅 = 1/𝑅_𝑆 + 1/𝑅_1 1/𝑅 = 1/9 + 1/2 1/𝑅 = (2 + 9)/18 1/𝑅 = 11/18 R = 18/11 Ω Case 6 R1 and R2 in parallel and R3 in series with them First we’ll find equivalent of R1 and R2 1/𝑅_𝑝 = 1/𝑅_1 + 1/𝑅_2 1/𝑅_𝑝 = 1/2 + 1/3 1/𝑅_𝑝 = (3 + 2)/6 1/𝑅_𝑝 = 5/6 𝑅_𝑝 = 6/5 Ω Now the circuit becomes R = Rp + R3 R = 6/5 + 6 R = (6 + 30)/5 R = 36/5 Ω Case 7 R1 and R3 in parallel and R2 in series with them First we’ll find equivalent of R1 and R3 1/𝑅_𝑝 = 1/𝑅_1 + 1/𝑅_3 1/𝑅_𝑝 = 1/2 + 1/6 1/𝑅_𝑝 = (3 + 1)/6 1/𝑅_𝑝 = 4/6 𝑅_𝑝 = 6/4 𝑅_𝑝 = 3/2 Ω Now the circuit becomes R = Rp + R2 R = 3/2 + 3 R = (3 + 6)/2 R = 9/2 Ω Case 8 R2 and R3 in parallel and R1 in series with them First we’ll find equivalent of R1 and R3 1/𝑅_𝑝 = 1/𝑅_2 + 1/𝑅_3 1/𝑅_𝑝 = 1/3 + 1/6 1/𝑅_𝑝 = (2 + 1)/6 1/𝑅_𝑝 = 3/6 𝑅_𝑝 = 1/2 𝑅_𝑝 = 2 Ω Now the circuit becomes R = Rp + R1 R = 2 + 2 R = 4 Ω Therefore, To give a total resistance of 4 Ω 3 Ω and 6 Ω in parallel and 2 Ω in series with them (b) To give a total resistance of 1 Ω Connect 2 Ω, 3 Ω and 6 Ω in parallel