Judge the equivalent resistance when the following are connected in parallel –
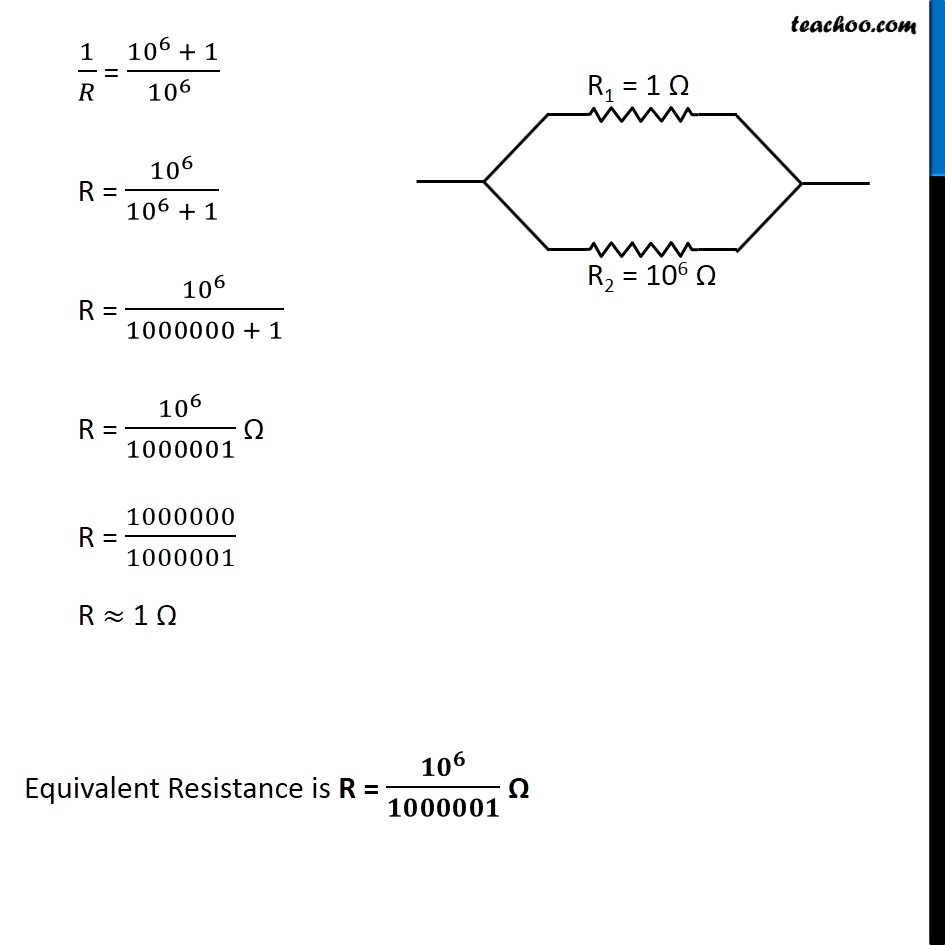
(a) 1 Ω and 10 6 Ω,
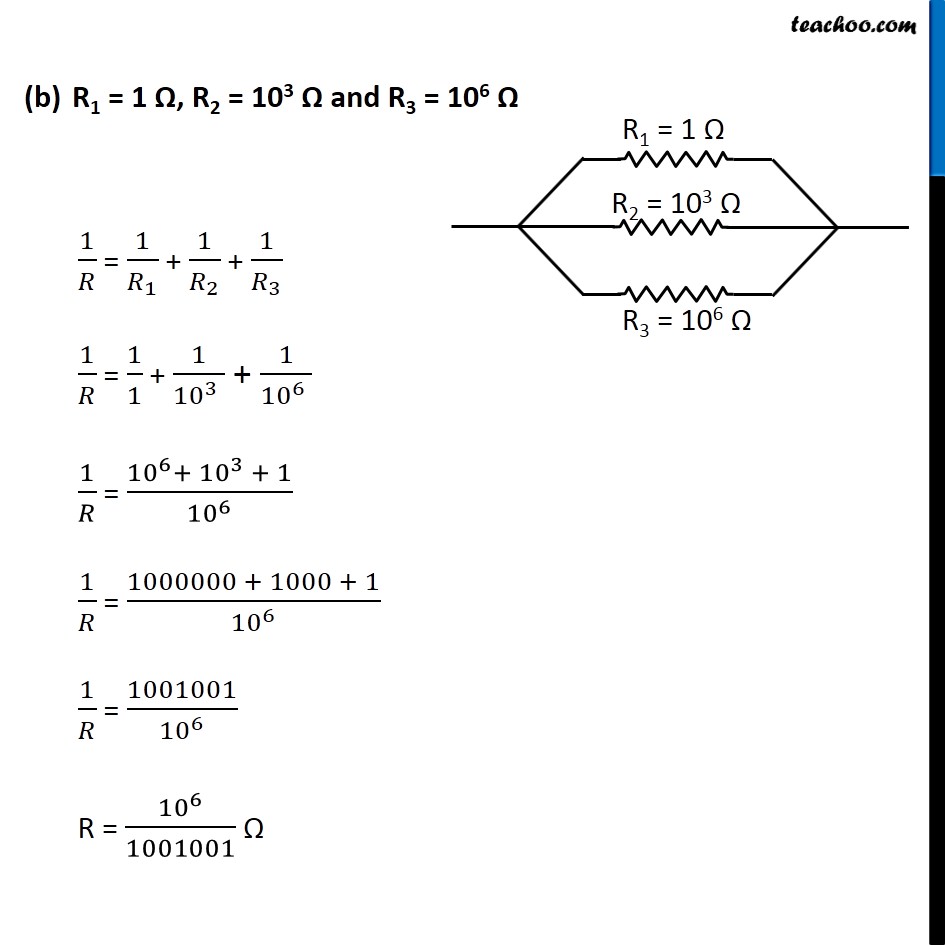
(b) 1 Ω and 10 3 Ω, and 10 6 Ω.


Questions from Inside the chapter
Questions from Inside the chapter
Last updated at December 16, 2024 by Teachoo




Transcript
Question 1 Page 216 Judge the equivalent resistance when the following are connected in - (a) 1 Ω and 106 Ω, (b) 1 Ω and 103 Ω, and 106 Ω.In a parallel connection, the equivalent resistance is given by 1/𝑅 = 1/𝑅_1 + 1/𝑅_2 + 1/𝑅_3 + … … … R1 = 1 Ω and R2 = 106 Ω 1/𝑅 = 1/𝑅_1 + 1/𝑅_2 1/𝑅 = 1/1 + 1/(〖10〗^6 ) 1/𝑅 = (〖10〗^(6 )+ 1)/(〖10〗^6 ) R = 〖10〗^6/(〖10〗^6 + 1) R = 〖10〗^6/(1000000 + 1) R = 〖10〗^6/1000001 Ω R = 1000000/1000001 R ≈ 1 Ω Equivalent Resistance is R = 〖𝟏𝟎〗^𝟔/𝟏𝟎𝟎𝟎𝟎𝟎𝟏 Ω R1 = 1 Ω, R2 = 103 Ω and R3 = 106 Ω 1/𝑅 = 1/𝑅_1 + 1/𝑅_2 + 1/𝑅_3 1/𝑅 = 1/1 + 1/(〖10〗^3 ) + 1/(〖10〗^6 ) 1/𝑅 = (〖10〗^6+ 〖10〗^3 + 1)/〖10〗^6 1/𝑅 = (1000000 + 1000 + 1)/〖10〗^6 1/𝑅 = 1001001/〖10〗^6 R = 〖10〗^6/1001001 Ω R = 1000000/1001001 R ≈ 0.999 Ω Equivalent Resistance is R = 〖10〗^6/1001001 Ω