Activity 11.15 - An object of mass 20 kg is dropped from a height of 4 m

Transcript

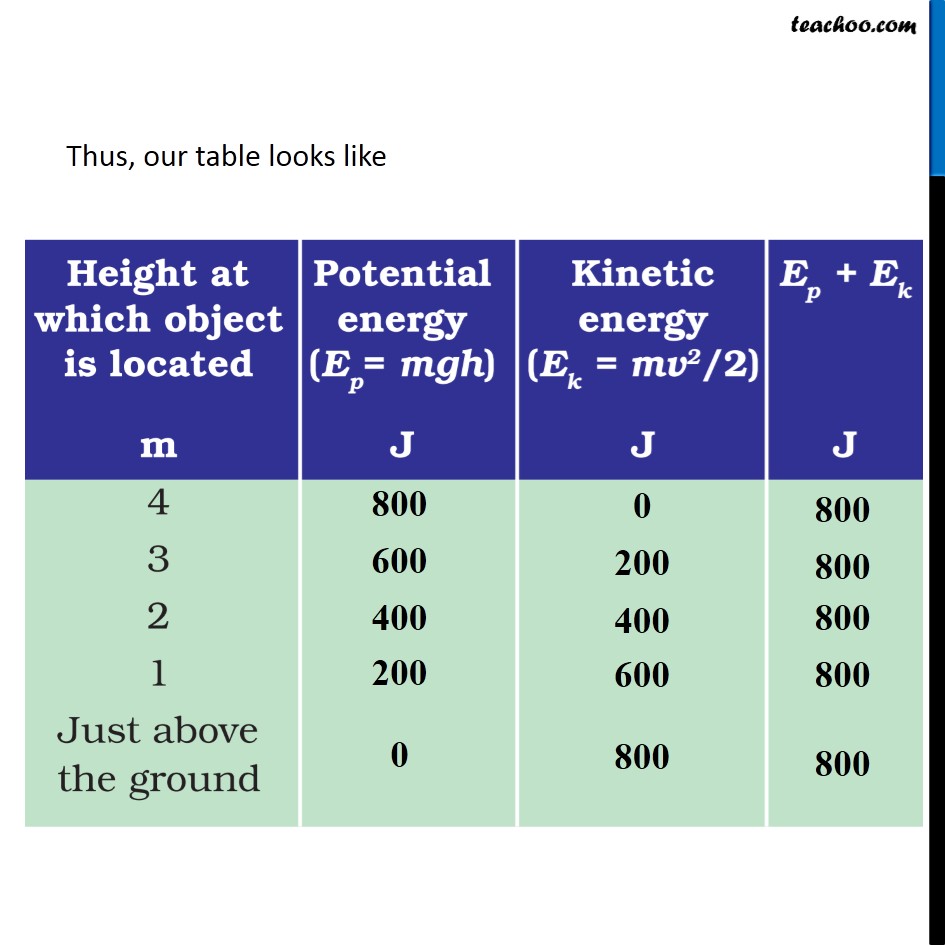
Activity 11.15 An object of mass 20 kg is dropped from a height of 4 m. Fill in the blanks in the following table by computing the potential energy and kinetic energy in each case. Take g = 10 m/s2 Mass of the object = m = 20 kg Acceleration due to gravity = g = 10 m/s2 At Height = 4 m Since the is just dropped, Velocity of the ball = v = 0 m/s Potential Energy Potential Energy = m × g × h Ep = 20 × 10 × 4 Ep = 800 J Kinetic Energy Kinetic Energy = 1/2 mv2 Ek = 1/2 × 20 × 02 Ek = 0 J Total energy = Ep + Ek = 800 + 0 = 800 J At Height = 3 m To find Potential Energy, we need height To find Kinetic Energy, we need velocity Finding Velocity Initial velocity = u = 0 m/s Acceleration = a = g = 10 m/s Distance travelled = s = 4 − 3 = 1 m We know u, a and s We can find v using 3rd equation of motion v2 − u2 = 2as (Velocity at highest point is 0) v2 − u2 = 2as v2 − 0 = 2 × 10 × 1 v2 = 20 Finding Potential and Kinetic Energy Potential Energy Potential Energy = m × g × h Ep = 20 × 10 × 3 Ep = 600 J Kinetic Energy Kinetic Energy = 1/2 mv2 Ek = 1/2 × 20 × 20 Ek = 200 J Total energy = Ep + Ek = 600 + 200 = 800 J At Height = 2 m To find Potential Energy, we need height To find Kinetic Energy, we need velocity Finding Velocity Initial velocity = u = 0 m/s Acceleration = a = g = 10 m/s Distance travelled = s = 4 − 2 = 2 m We know u, a and s We can find v using 3rd equation of motion v2 − u2 = 2as (Velocity at highest point is 0) v2 − u2 = 2as v2 − 0 = 2 × 10 × 2 v2 = 40 Finding Potential and Kinetic Energy Potential Energy Potential Energy = m × g × h Ep = 20 × 10 × 2 Ep = 400 J Kinetic Energy Kinetic Energy = 1/2 mv2 Ek = 1/2 × 20 × 40 Ek = 400 J Total energy = Ep + Ek = 400 + 400 = 800 J At Height = 1 m To find Potential Energy, we need height To find Kinetic Energy, we need velocity Finding Velocity Initial velocity = u = 0 m/s Acceleration = a = g = 10 m/s Distance travelled = s = 4 − 1 = 3 m We know u, a and s We can find v using 3rd equation of motion v2 − u2 = 2as (Velocity at highest point is 0) v2 − u2 = 2as v2 − 0 = 2 × 10 × 3 v2 = 60 Finding Potential and Kinetic Energy Potential Energy Potential Energy = m × g × h Ep = 20 × 10 × 1 Ep = 200 J Kinetic Energy Kinetic Energy = 1/2 mv2 Ek = 1/2 × 20 × 60 Ek = 600 J Total energy = Ep + Ek = 200 + 600 = 800 J Just above the ground (h ≈ 0 m) To find Potential Energy, we need height To find Kinetic Energy, we need velocity Finding Velocity Initial velocity = u = 0 m/s Acceleration = a = g = 10 m/s Distance travelled = s = 4 − 0 = 4 m We know u, a and s We can find v using 3rd equation of motion v2 − u2 = 2as (Velocity at highest point is 0) v2 − u2 = 2as v2 − 0 = 2 × 10 × 4 v2 = 80 Finding Potential and Kinetic Energy Potential Energy Potential Energy = m × g × h Ep = 20 × 10 × 0 Ep = 0 J Kinetic Energy Kinetic Energy = 1/2 mv2 Ek = 1/2 × 20 × 80 Ek = 800 J Total energy = Ep + Ek = 0 + 800 = 800 J Thus, our table looks like