NCERT Question 18 - Chapter 10 Class 9 - Gravitation

Transcript

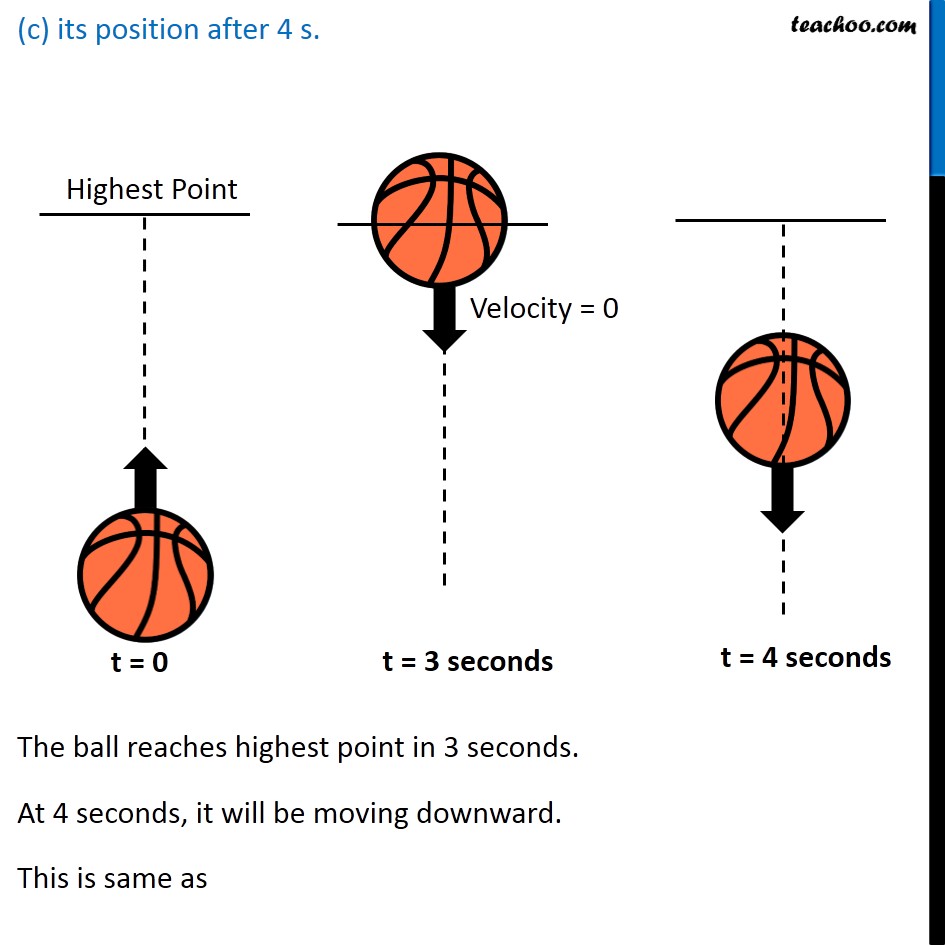
NCERT Question 18 A ball thrown up vertically returns to the thrower after 6 s. Find (a) the velocity with which it was thrown up, (b) the maximum height it reaches, and (c) its position after 4 s. Max Height Reaches Highest Point Max Height And comes back to the same point Total Time Taken = 6 seconds Since it takes 6 seconds for the ball to return Therefore, ∴ Time taken to reach maximum height = 6/2 = 3 seconds Now, solving all parts the velocity with which it was thrown up, We need to find Initial Velocity Let Initial velocity = u At the highest point of motion, velocity becomes 0 Therefore Final velocity = v = 0 m/s And Acceleration = −g = −9.8 m/s2 Time = 3 seconds We know v, a and t (Acceleration is negative because ball is thrown upwards) Finding u by 1st equation of motion v = u + at 0 = u + (−9.8) (3) 0 = u − 29.4 u = 29.4 m/s Thus, initial velocity is 29.4 m/s (b) the maximum height it reaches, and Calculating maximum height (s) We know u, t and at Finding distance using 2nd equation of motion s = ut + 1/2 at2 = 29.4 × 3 + 1/2 (−9.8) (3)2 = 88.2 − 1/2 × 9.8 × 9 = 88.2 − 44.1 = 44.1 m Thus, maximum height it reaches is 44.1 m (c) its position after 4 s. The ball reaches highest point in 3 seconds. At 4 seconds, it will be moving downward. This is same as A ball is dropped from highest point We need to calculate distance it moves in 1 second When ball is dropped, Initial velocity = 0 m/s Time = 1 second Acceleration = g = 9.8 m/s We need to find s We know u, a and t Finding s using 2nd equation of motion. s = ut + 1/2 at2 s = 0 × 1 + 1/2 × 9.8 × (1)2 (Positive acceleration as it is moving down) s = 9.8/2 s = 4.9 m So, Position of ball is 4.9 from the top Therefore, ∴ The initial velocity of the ball is 29.4 m/s The maximum height it reaches is 44.1 m It’s position of ball at t = 4s is 4.9 m (from top) (from the top)